An Accessible Derivation of Linear Regression
Technical disclaimer: It is possible to derive a model without normality assumptions. We'll go down this route because it's straightforward enough to understand and by assuming normality of the model's output, we can reason about the uncertainty of our predictions.
This post is intended for people who are already aware of what Linear Regression is (and maybe have used it once or twice) and want a more principled understanding of the math behind it.
Some background in basic probability (probability distributions, joint probability, mutually exclusive events), linear algebra, and stats is probably required to make the most of what follows. Without further ado, here we go:
The Machine Learning world is full of amazing connections: the exponential family, regularization and prior beliefs, KNN and SVMs, Maximum Likelihood and Information Theory – it's all connected! (I love Dark). This time we'll discuss how to derive another one of the members of the exponential family: the Linear Regression model, and in the process we'll see that the Mean Squared Error loss is theoretically well motivated. As with any regression model, we'll be able to use it to predict numerical, continuous targets. It's a simple yet powerful model that happens to be one of the workhorses of statistical inference and experimental design. However we will be concerned only with its usage as a predictive tool. No pesky inference (and God forbid, causal) stuff here.
Alright, let us begin. We want to predict something based on something else. We'll call the predicted thing y and the something else x. As a concrete example, I offer the following toy situation: You are a credit analyst working in a bank and you're interested in automatically finding out the right credit limit for a bank customer. You also happen to have a dataset pertaining to past clients and what credit limit (the predicted thing) was approved for them, together with some of their features such as demographic info, past credit performance, income, etc. (the something else).
So we have a great idea and write down a model that explains the credit limit in terms of those features available to you, with the model's main assumption being that each feature contributes something to the observed output in an additive manner. Since the credit stuff was just a motivating (and contrived) example, let's go back to our pure Math world of spherical cows, with our model turning into something like this:

We still have the predicted stuff (y) and the something else we use to predict it (x). We concede that some sort of noise is unavoidable (be it by virtue of imperfect measuring or our own blindness) and the best we can do is to assume that the model behind the data we observe is stochastic. The consequence of this is that we might see slightly different outputs for the same input, so instead of neat point estimates we are "stuck" with a probability distribution over the outputs (y) conditioned on the inputs (x):

Every data point in y is replaced by a little bell curve, whose mean lies in the observed values of y, and has some variance which we don't care about at the moment. Then our little model will take the place of the distribution mean.
Assuming all those bell curves are actually normal distributions and their means (data points in y) are independent from each other, the (joint) probability of observing the dataset is

Logarithms and some algebra to the rescue:

Logarithms are cool, aren't they? Logs transform multiplication into sum, division into subtraction, and powers into multiplication. Quite handy from both algebraic and numerical standpoints. Getting rid of constant stuff, which is irrelevant in this case, we arrive to the following maximum likelihood problem:

Well, that's the same as

The expression we are about to minimize is something very close to the famous Mean Square Error loss. In fact, for Optimization purposes they're equivalent.
So what now? This minimization problem can be solved exactly using derivatives. We'll take advantage of the fact that the loss is quadratic, which means convex, which means one global minima; allowing us to take its derivative, set it to zero and solve for theta. Doing this we'll find the value of the parameters theta that makes the derivative of the loss zero. And why? because it is precisely at the point where the derivative is zero, that the loss is at its minimum.
To make everything somewhat simpler, let's express the loss in vector notation:

Here, X is an NxM matrix representing our whole dataset of N examples and M features and y is a vector containing the expected responses per training example. Taking the derivative and setting it to zero we get

There you have it, the solution to the optimization problem we have cast our original machine learning problem into. If you go ahead and plug those parameter values into your model, you'll have a trained ML model ready to be evaluated using some holdout dataset (or maybe through cross-validation).
If you think that final expression looks an awful lot like the solution of a linear system,

it's because it does. The extra stuff comes from the fact that for our problem to be equivalent to a vanilla linear system, we'd need an equal number of features and training examples so we can invert X. Since that's seldom the case we can only hope for a "best fit" solution – in some sense of best – resorting to the Moore-Penrose Pseudoinverse of X, which is a generalization of the good ol' inverse matrix. The associated _wikipedia_ entry makes for a fun reading.
A Small Incursion into Regularization
From now on I'll assume you may have heard the term "regularization" somewhere and maybe you know what it means. In any case I'll tell you how I understand it: regularization is anything you do to a model that makes its out-of-sample performance better at the expense of a worse in-sample performance. Why is this even a thing? because in the end, out of sample (i.e. real life) performance is what matters – no one is gonna care how low your training error is, or how amazing your AUC is on the training set unless your model performs comparatively well in production. And we have found that if we are not careful we will run into something called overfitting, where your model memorizes the training set all the way down to the noise, becoming potentially useless for out of sample predictions. We also know that there is a trade-off between model complexity and out of sample performance (Vapnik's statistical learning theory) and regularization can be seen as an attempt to keep model complexity under control in the hope of achieving better generalization abilities (here generalization is another name for out of sample performance).
Regularization can take many forms, but for the purposes of this article we'll only discuss one approach that is often used for linear regression models. Remember I said that with regularization we are trying to keep complexity under control, right? Well, unwanted complexity can creep in mainly via two ways: 1. too many input features and 2. large values for their corresponding theta values. It turns out that something called L2 regularization can help with both. Remember our loss?

we were only concerned to minimize the squared differences between predicted and observed values of y, without regard for anything else. Such myopic focus could be a problem because you could in principle game the system and keep adding in features till the error is minuscule, even if those extra features have nothing to do with the signal we are trying to learn. If we had perfect knowledge about the things that are relevant for our problem, we wouldn't include useless features! (to be fair we wouldn't be using machine learning on the first place but i digress). To compensate for our ignorance and mitigate the risk of introducing said unwanted complexity, we'll add an extra term to the loss:

What does that do, you might ask. I'll tell you – we've just introduced an incentive to keep the magnitude of the parameters as close to zero as possible. In other words we want to keep complexity at a minimum. Now instead of having just one objective (the minimization of prediction errors), we've got one more (minimization of complexity), and the solution for the overall problem will have to balance both. We do have a say in how that balance looks like, through that shiny new lambda coefficient: the larger it is, the more importance we give to the low complexity target.
That's a lot of talk. Let's see what the extra term does to the optimal theta. The new loss in vectorized form is
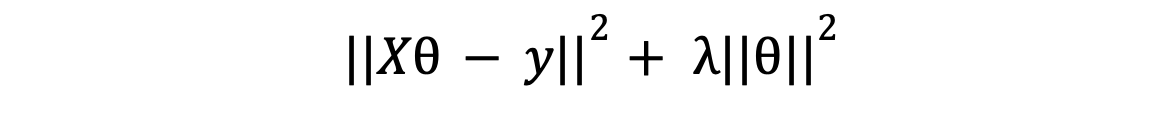
taking its derivative, setting it to zero and solving for theta:

It turns out that the new solution is not too different from the previous one. We've got an extra diagonal matrix which is going to take care of any rank issues that would prevent us from inverting the XTX matrix, by adding some "jitter" into the mix. That illuminates another way in which unnecessary complexity might be introduced: collinear features, that is, features that are linear transformations (scaled and shifted versions) of other features. As far as linear regression cares, two collinear features are the same feature, count as only one column, and the extra feature doesn't add any new information to help train our model; rendering the XTX matrix rank-deficient, i.e. impossible to invert. With regularization, in every row of XTX, a different column is affected by lambda, the jitter – stopping any possible collinearity and making it full-rank. We see that adding random crap as predictors could actually ruin the whole learning process. Thankfully regularization is here to save the day (please don't misconstrue my praise of regularization as an invitation to be careless when selecting your predictors – it's not).
So there you have it, a regularized linear regression model ready to use. Where do we go from here? well, you could expand on the idea that regularization encodes a prior belief about the parameter space, revealing its connection with Bayesian inference. Or you could double down on its connection with Support Vector Machines and eventually with non-parametric models like KNN. Also, you could ponder about the fact that all those fancy gradients from linear and logistic regression look suspiciously similar. Rest assured I'll be touching on those subjects in a future post!

