Data Science for Schools, Part 2: Student Electives Allocation with Python

Author:Murphy | View: 30017 | Time: 2025-03-22 21:05:28

Imagine the following scenario: you're a teacher, and you've been asked to help with creating an extra-curricular "options/electives" programme for 200 students.

Each student selects their top 4 preferences, and you need to allocate the students in a way that maximises student satisfaction, while accounting for various constraints (e.g., an elective needs a minimum of 5 students to run).

How do you do it?

Data science for schools

In this article, I'll show you how to use Data Science – specifically, a technique called linear programming – to solve this problem.

It's part of a broader series in which I'm showcasing a few ways that schools can apply data science and AI to improve things like:

timetabling
assessments
lesson plans

My aim is to help you automate the boring stuff and free up time for teachers to focus on what they do best: teach.

Why should I care (if I'm not a teacher)?

As I've previously argued, data scientists are way too obsessed with machine learning:

Stop Overusing Scikit-Learn and Try OR-Tools Instead

In this article, we'll use a technique called Linear Programming, which is a nifty way to take constraints like:

"Each student must be allocated to one of their top 4 choices"
"If a student was allocated to Football in Fall Semester, they're ineligible to be allocated to Football in Spring Semester"

… and translate them into mathematical equations that can then be solved programmatically.

Linear Programming is hugely valuable skill to have in your data science toolkit. If you want to create a unique portfolio and learn a high-value (but low-supply) data skill, this is an excellent place to start.

My previous guide kicked things off by showing how to use Python to automatically arrange cover for lessons where the usual teacher was absent:

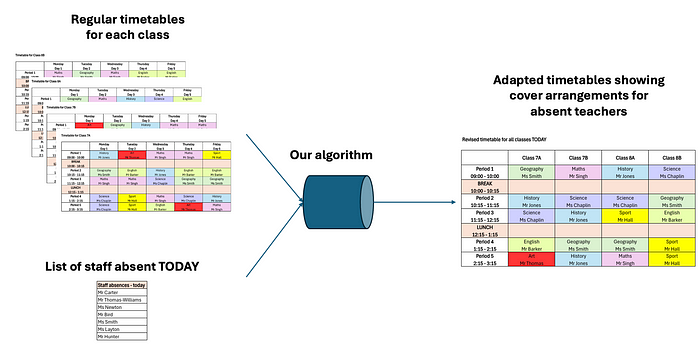
Image from my previous article, Data Science for Schools, Part 1

In this guide, we'll build on that foundation and introduce some more complex constraints.

Part 1: Create data

Before we get started with the optimisation, we'll need to set up our environment and create some data.

First, we'll import the libraries we'll need:

import numpy as np
import pandas as pd
from collections import Counter
from faker import Faker
from ortools.sat.python import cp_model
from ortools.linear_solver import pywraplp

Next, let's create a DataFrame called options which lists the electives being offered and their maximum capacity:

# Define dict of options
# Format: {option: max_capacity}
options_dict = {
    "Badminton": 20,
    "Football 1": 28,
    "Football 2": 28,
    "Basketball": 15,
    "Cricket": 22,
    "Basket Weaving": 20,
    "Lego Engineering": 20,
    "History Guided Reading": 20,
    "Learn a Brass Instrument": 10,
    "Public Speaking": 15,
    "Knitting": 15,
    "Karate": 15,
}

# Convert to DataFrame and insert id column
options = pd.DataFrame(list(options_dict.items()), columns=['Option', 'Maximum capacity'])
options.insert(0, 'option_id', range(1, len(options)+1))
options

Next, we'll create 200 fake students, using the library Faker to programmatically create realistic names:

# Create 200 student IDs
student_ids = [_ for _ in range(1, 201)]

# Create 200 student names
fake = Faker()
student_names = [f"{fake.first_name()} {fake.last_name()}" for _ in student_ids]

# Store in a DataFrame
students = pd.DataFrame({
    'student_id': student_ids,
    'student_name': student_names,
})

students

Let's now create the students' preferences and add these into the students DataFrame. For now, we'll assume that the preferences are random (later, we'll revise this, to make it more realistic):

# Create preferences
preferences_dict = {student: np.random.choice(options['option_id'], size=4, replace=False) for student in student_ids}
preferences = pd.DataFrame.from_dict(preferences_dict, orient='index', columns=[f'Preference {i}' for i in range(1, 4+1)])
preferences.index.name = 'student_id'
preferences.reset_index(inplace=True)

# Merge
students = pd.merge(students, preferences, on='student_id')
students

Finally, we'll add a quick check to make sure that there is enough capacity across the electives to ensure that every student can be allocated:

num_students = students.shape[0]
num_electives = options.shape[0]

print(f"Number of students: {num_students}")
print(f"Number of electives: {num_electives}")

# Check that there's enough capacity for all the students
assert sum(options_dict.values()) >= len(students)

# Number of students: 200
# Number of electives: 12

Part 2: Simple allocation

We've got our data; now, we can start the allocation process.

We'll start by building a simple model that allocates each student to an elective option while maximising student satisfaction (i.e., the model will try to give as many students their first choice as possible and try to avoid assigning students their lower-ranked choices).

Here are the assumptions:

Each student will be assigned to exactly one elective.
Each student must be assigned to one of their top 4 preferences.
Each option can only be selected once, but there are no dependencies or incompatible combinations. (If a student picks Football 1 as their first choice, it doesn't preclude them from picking any of the other options – e.g., Football 2 – and so on.)

Later, we'll add some more complex considerations. But this will be a good start.

Initialise the model

First, initialise the model using OR-Tools:

solver = pywraplp.Solver.CreateSolver('SCIP')

Create decision variables

Next, we'll create 2,400 Boolean decision variables – one for each student-elective combination (12 students * 200 electives = 2,400 variables):

# Decision variables
decis_vars = {}
for i in students['student_id']:
    for j in options['option_id']:
        decis_vars[f'student{i}_elective{j}'] = solver.BoolVar(f'student{i}_elective{j}')

print(f"Number of decision variables = {solver.NumVariables()}")

For example, for Student 1 ("David Gilbert"), there will be 12 decision variables, each of which represents a possible elective allocation:

[k for k in decis_vars.keys() if k.startswith('student1_')]

# Result
['student1_elective1',
 'student1_elective2',
 'student1_elective3',
 'student1_elective4',
 'student1_elective5',
 'student1_elective6',
 'student1_elective7',
 'student1_elective8',
 'student1_elective9',
 'student1_elective10',
 'student1_elective11',
 'student1_elective12']

If David is allocated to Elective 1 ("Badminton"), the variable student1_elective1 will be set to 1, and the 11 other variables will be set to 0. If David is allocated to Elective 2 ("Football 1"), the variable student1_elective2 will be set to 1, and the remaining 11 will be set to 0. And so on.

(Remember: we don't know in advance which elective David will be allocated to. The goal of our optimisation workflow is to work out how to allocate all the students in an optimal way. For now, we initialise these variables as Boolean variables, which means "these decision variables could equal 0, or they could equal 1".)

Add constraints

Next we'll add the constraints to our model:

# Define the constraints

# 1. Constraint #1: Each student can only be assigned to one elective option
for student_id in students['student_id']:

    # Collect the decision variables related to that student
    relevant_variables = []
    for d in decis_vars.keys():
        if d.startswith(f'student{student_id}_'):
            relevant_variables.append(decis_vars[d])

    # Add the constraint
    solver.Add(sum(relevant_variables) == 1)

# 2. Constraint #2: Each student must be assigned to one of their top 4 preferences
for student_id in students['student_id']:

    # Identify the student's top preferences
    preferences = list(preferences_dict[student_id])

    relevant_variables = []
    for p in preferences:
        for d in decis_vars.keys():
            if d.startswith(f'student{student_id}_') and d.endswith(f'elective{p}'):
                relevant_variables.append(decis_vars[d])

    # Add the constraint
    solver.Add(sum(relevant_variables) == 1)

# 3. Constraint #3: Each elective has a max upper limit
for option in options['option_id']:

    max_num_students = options[options['option_id']==option]['Maximum capacity'].values[0]
    relevant_variables = []
    for d in decis_vars.keys():
        if d.endswith(f'elective{option}'):
            relevant_variables.append(decis_vars[d])

    # Add the constraint
    solver.Add(sum(relevant_variables) <= max_num_students)

Define the objective function

The objective function is the thing we want to maximise (or minimise).

In plain English, our objective function is: "allocate students in a way that maximises student satisfaction, while still meeting all the constraints."

We can also express this mathematically:

If that looks like gobbledygook, don't worry! One of the reasons Linear Programming is less famous (relative to, e.g., machine learning) is because it hides behind scary mathematical notation which can look a bit intimidating to newcomers. But you don't need to understand the mathematical notation to be able to understand the principles and write the code:

# Define the objective function
objective = solver.Objective()

for index, row in students.iterrows():

    # Fetch the student id
    student_id = row['student_id']

    # Identify the student's top 4 preferences
    for pref_rank in range(1, 5):
        preference = row[f'Preference {pref_rank}']

        # Find the option that corresponds to the preference
        for option_index, option_row in options.iterrows():
            option_id = option_row['option_id']

            if option_id == preference:

                # Find the decision variable for this student and option
                var_name = f'student{student_id}_elective{option_id}'
                if var_name in decis_vars:
                    var = decis_vars[var_name]
                    # Add to the objective function with a weight based on preference rank
                    objective.SetCoefficient(var, 5 - pref_rank)  # Higher preference ranks are weighted more positively

objective.SetMaximization()

Solve

We've initialised our decision variables, defined our constraints, and specified our objective function. Now, let's find the optimal solution:

status = solver.Solve()

# Check if the problem has an optimal solution
if status == pywraplp.Solver.OPTIMAL:
    print('Optimal solution found!')

    # Print optimal objective value
    print('Objective value =', solver.Objective().Value())

# Optimal solution found!
# Objective value = 785.0

Show solution

Our algorithm has successfully managed to allocate all the students in a way that satisfies our constraints and maximises student satisfaction. Woo hoo! Now, we need to see the solution.

We could just check the value of each individual decision variable:

for var in decis_vars.values():
    print(var.solution_value())

… but that would get tedious! Let's define some helper functions to print out the results and get some useful statistics:

def get_relevant_vars(student_id):
    """Find the (12) decision variables related to a given `student_id`."""
    return {k: v for k, v in decis_vars.items() if f'student{student_id}' in k}

def show_elective(list_of_vars):
    """For a given list of decision variables, find the one(s) equal to 1."""
    vars_equal_to_1 = [k.split('elective')[1] for k, v in list_of_vars.items() if v.solution_value() == 1]
    return vars_equal_to_1[0]

def get_final_allocations(list_of_student_ids=students['student_id']):
    """For a given `list_of_student_ids`, retrieve the final allocations."""
    final_allocations = {student: show_elective(get_relevant_vars(student)) for student in list_of_student_ids}
    return final_allocations

def count_final_allocations(allocations_dict):
    """Count the number of student allocated to each elective."""
    return Counter(allocations_dict.values())

def count_num_students_who_got_each_choice():
    """Count how many students got their 1st choice, how many got their second, etc."""       

    satisfaction = {}
    for student in students['student_id']:
        allocated_elective = final_allocations[student]

        for i in range(1, 5):
            choice = students[students['student_id']==student][f'Preference {i}'].values[0]

            if allocated_elective == str(choice):
                satisfaction[student] = i

    return satisfaction

This will let us produce three things: (1) a dictionary showing where each student was allocated:

final_allocations = get_final_allocations()
final_allocations

# {1: '10',
#  2: '6',
#  3: '12',
#  4: '4',
#  5: '3',
#  6: '1',
#  7: '5',
#  ...
#  200: '9'}

… (2) the total number of students allocated to each elective:

count_final_allocations(final_allocations)

# Result
Counter({'5': 22,
         '6': 20,
         '8': 20,
         '7': 20,
         '1': 19,
         '3': 16,
         '10': 15,
         '12': 15,
         '4': 15,
         '11': 15,
         '2': 13,
         '9': 10})

… and (3) the number of students who got their 1st choice, 2nd choice, and so on:

performance = Counter(count_num_students_who_got_each_choice().values())

for i in range(1, 5):
    print(f"The number of students who got their #{i} choice was {performance[i]}")

# Result
# The number of students who got their #1 choice was 176
# The number of students who got their #2 choice was 24
# The number of students who got their #3 choice was 0
# The number of students who got their #4 choice was 0

From that, we can see that our algorithm did pretty well: 176 out of 200 students got their first preference, and the remaining 24 got their second preference. Not bad!

Part 3: More realistic voting preferences

So far, we've been assuming that student preferences are random, as though a student is equally likely to select Football and Basket weaving.

In reality, however, some options are likely to be heavily oversubscribed, and others undersubscribed.

Let's update our student preferences to account for this. Instead of this line:

preferences_dict = {student: np.random.choice(options['option_id'], size=4, replace=False) for student in student_ids}

We'll write:

preferences_dict = {student: np.random.choice(options['option_id'], size=4, replace=False, p=[0.05, 0.25, 0.25, 0.1, 0.05, 0.05, 0.05, 0.05, 0.1, 0.01, 0.01, 0.03]) for student in student_ids}

We're using the p parameter to specify the probability of choosing each option. I've weighted Football 1 and Football 2 the highest. This means that (unsurprisingly), these will have the most number of votes:

temp_df = students['Preference 1'].value_counts().to_frame()
temp_df.index.name = 'option_id'
temp_df.reset_index(inplace=True)

pd.merge(
    temp_df,
    options,
    on='option_id'
)

Now, if we run through the optimisation code again, we'll see that the algorithm still found an optimal solution, but fewer people were allocated to their top choice:

performance = Counter(count_num_students_who_got_each_choice().values())

for i in range(1, 5):
    print(f"The number of students who got their #{i} choice was {performance[i]}")

# Result
# The number of students who got their #1 choice was 143
# The number of students who got their #2 choice was 51
# The number of students who got their #3 choice was 6
# The number of students who got their #4 choice was 0

Part 4: Additional constraints

The model is looking good, but it's still a bit too simplistic to be useful in the real world.

Let's rectify this by adding an additional constraint:

Each elective needs a minimum of 5 students to be viable. If it has less than 5, it won't run, and the students will need to be allocated elsewhere.

To make these changes, add the following lines to the Constraints section of your code (just before we define the objective function):

# 4. Each elective needs a minimum of 5 students to run
min_num_students = 5
for option in options['option_id']:

    relevant_variables = []
    for d in decis_vars.keys():
        if d.endswith(f'elective{option}'):
            relevant_variables.append(decis_vars[d])

    # Add the constraint
    solver.Add(sum(relevant_variables) >= min_num_students)

Any feedback?

I hope you found this helpful – if you've got any further ideas or suggestions for what I should cover in this series, please let me know! I want to make this as useful as possible.

One more thing –

I write a data/AI newsletter called AI in Five, and I also make website templates over at MakePage.org. If you're looking for a new portfolio template, check it out!