From Surrogate Modelling to Aerospace Engineering: a NASA Case Study

Imagine that you are going to the doctor because you have abdominal pain. Imagine that, in order to tell you the reason for your pain, the doctor needs to run a numerical simulation. This numerical simulation solves the differential equation of your body and the approximation error is so low that it results in basically 100% accuracy: you will know exactly why you have that abdominal pain, with no room for error at all (I know this sounds crazy, but bear with me here). Would you use the numerical simulation? Of course you would, why not?

Now imagine that, because this numerical simulation solves very complicated differential equations, to get the response from the computer you need to wait 35 years of GPU runtime. This would immediately drop the attractiveness of the method. What is the use of this method if it takes so long to get the response out of it? Sure, it might be 100% accurate, but the computational cost to pay is too large.

Well, engineers thought of a solution. This solution is called surrogate modelling. As the name says, the approach is to use a surrogate of the original simulation. It is also a model, meaning that it aims to replicate the result of the original system but in a fraction of the GPU resources and computational time. Of course, surrogate models are not perfect and they result in a loss of accuracy with respect to the original method, but the computational time is incredibly smaller and it turns non feasible studies into feasible ones.

In Aerospace Engineering, surrogate model is intensively used. This is because the surrogate models help to understand the parameters of a problem and allow the designers to select the variables that are actually interesting and the ones that can be discarded for a specific problem.

In this blogpost, I will give a general idea of surrogate models, from theory to code. Then, I will describe a specific NASA application of surrogate models coming from their own paper. Let's get it started!

1. About Surrogate Models

Let's assume we have to predict how much, in terms of mass, we can deliver using a space vehicle. To do that you need to solve a very complicated differential equation of the vehicle trajectory. Based on the vehicle trajectory we can extrapolate the so called payload delivered.

Now, this equation has multiple parameters. As a start, let's consider only three parameters: number of engines, the thrust per engine, or the tank cylinder length.

A (amazing) differential equation numerical solver is called "Finite Element Method" or "Finite Element Model" (FEM). FEM solves differential equations numerically by discretizing the physical space of interest and then applying the differential equation across this discretized space. This approach leads to a very good approximation of reality but at a large computational and time cost. Usually, FEMs run on clusters of GPUs that, as you can imagine, tend to be expensive and time consuming.

For example, let's assume that each simulation takes 10 minutes, and let's consider the three-dimensional parameter space:

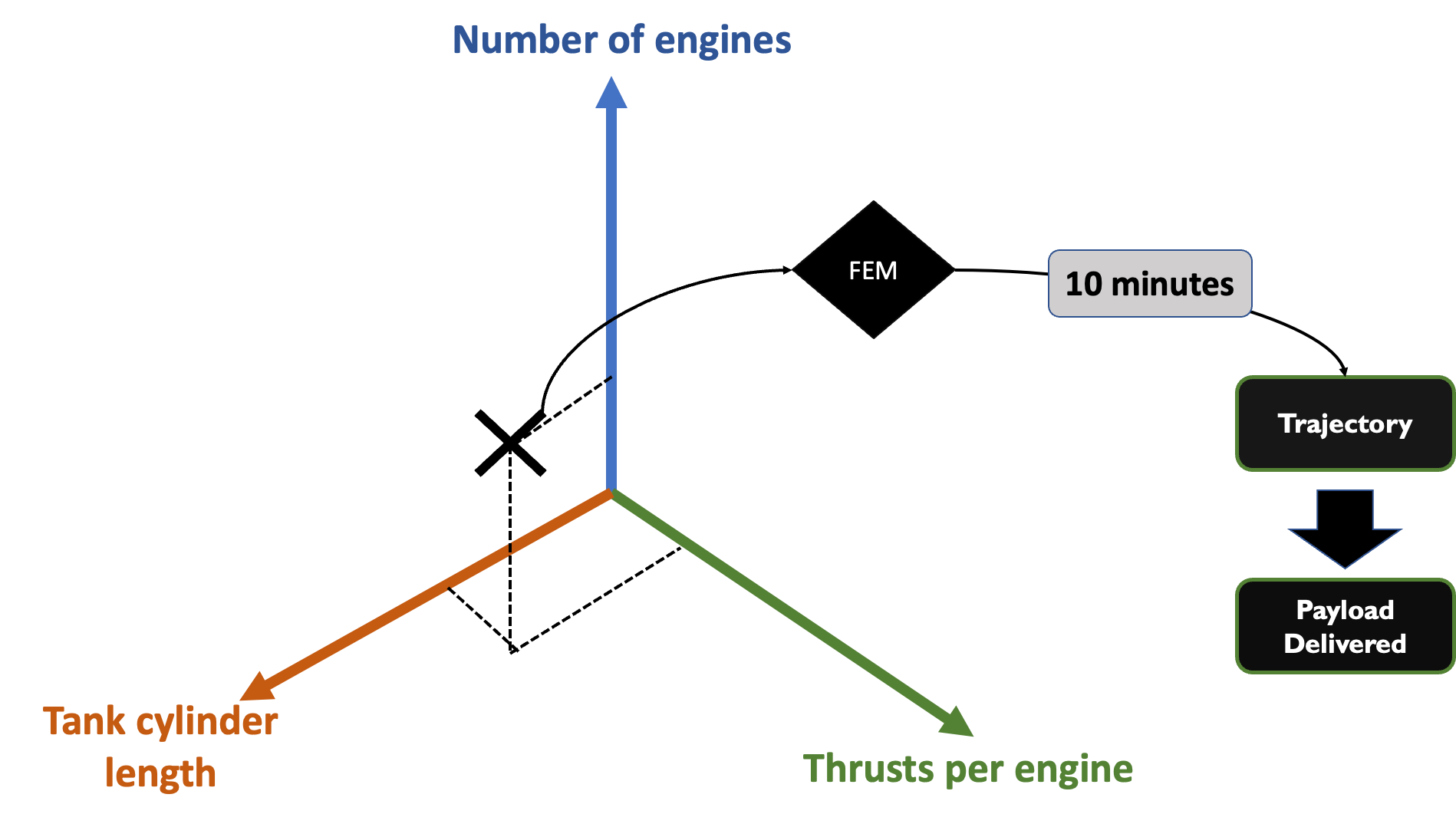
So you give me the parameters, I take 10 minutes of your time, use the FEM and give you the trajectory of the vehicle and then estimate the payload delivered.

Beautiful, now let's say that we want to explore this parameter space. If we consider 10 steps per parameter (0, 0.1,0.2,…,1), we have to run 10³ = 1000 simulations, which is:

Now, if the number of parameters is 4 it gets 10⁴ = 10,000 simulations, with 100,000 minutes that require 70 days. And that's only for 10 steps. If we consider 100 steps and only 4 parameters we are talking about 7000 days, which is around 20 years. I think you are getting the gist.

Now the problem with this is the 10 minutes waiting time. If you replace 10 minutes with 0.4 ms, you are already much more at ease and those kinds of computations become much more doable.

So how do we achieve this "surrogate model"? The idea is that we will run a limited amount of FEM experiments. These experiments will form the database that we will use to train the surrogate model, which will be a machine learning model (spoiler). Then we evaluate the quality: if the quality is satisfactory we are good to go and use the surrogate model as we please, if the quality is not satisfactory we have to go back and re-sample the parameter space and re-train the surrogate model.

I know it's confusing, and I think that the best way to clear all the confusion is by actually building our surrogate model. Let's get started!

1.1 Design of Experiment

Ok, fine, we won't be able to run maybe 100,000 simulations (because we don't want to wait 70 days), but maybe waiting 7 days to have a solid run of 10,000 samples is a good start. So let's say we want to do it. How do we even do it?

We have this problem that we want to get as much information as we can to train a Machine Learning model (spoiler) but we don't want to wait 70 days to run an insanely large amount of simulations. This part of the process is named Design of Experiment (DoE) or more simply *"sampling".**

*I wrote a blog post about it, you can find it here

There are a lot of sampling techniques. One of the most used in surrogate modeling is called Latin Hypercube Sampling (LHS), and it aims to get the best from both random techniques and more structured approaches like uniform sampling. The code to do a LHS sampling is super simple but requires a library named "smt". You can install it like this:

pip install smt

And this is the result:

1.2. Surrogate Model selection and training

After you sample the original parameter space, we can use the same smt library to train a machine learning model. Remember that you usually have only a limited amount of points, so you might want to try to hit the problem with very simple models rather than super complicated algorithms like Neural Networks.

For example, a fairly simple model that has good performance even with few points as a dataset is Radial Basis Function (RBF). RBF models predict outcomes by combining weighted radial functions centered at each data point, often using Gaussian functions. This approach is effective because it captures the local variations in the data, and it provides smooth interpolations even when the dataset is small.

I used a lot of big words, but the truth of the matter is that everything can be implemented in a very few lines of code:

1.3. Quality Assessment

Now that we have done the DoE and trained our surrogate model, the last thing to do is to assess the quality of our method.

Given a certain threshold of quality (e.g. a Mean Squared Error that is smaller than 0.02), we assess if, on the test set, our surrogate model is smaller or equal to that value. If the answer is yes, then we are good to go. If not we have to resample the parameter space.

We usually have two options. We either resample with another LHS, for example, or another "static" method, or we do some "adaptive sampling" strategy. Adaptive sampling aims to sample the area where the error (or the uncertainty) of the surrogate model is larger. After the resampling stage is done, we can retrain our surrogate model and assess the quality again. We repeat these two steps until we converge to the desired level of quality.

2. The NASA Case Study

I don't want this "surrogate model" thing to sound like a computer science experiment for nerds like me. Mainly because it is not.

In 2016, NASA released a case study on how they are using surrogate models, in their own words, "to provide customers with a full vehicle mass breakdown to tertiary subsystems, preliminary structural sizing based upon worst-case flight loads, and trajectory optimization to quantify integrated vehicle performance for a given mission". Confusing enough right? Let's describe it step by step.

2.1 The need for Surrogate Models in Aerospace

When dealing with real life engineering products, the decisions made during early conceptual design have a large impact on the expected life-cycle cost. In the example that we saw earlier, we notice that if we need to explore a 3-dimensional space with 10 steps we need way less time than what we would need if we explore a 10-dimensional space.

In the specific case of NASA, given a set of parameters of a vehicle, the analytics team of Advanced Concept Office (ACO) utilizes a proven set of tools to:

• Provide customers with a full vehicle mass breakdown of the vehicle
• Do preliminary structural sizing (which is an estimate of the liftoff weight) based on worst-case flight loads
• Perform a trajectory optimization to quantify integrated vehicle performance for a given mission

So using the NASA system we get, for a given set of parameters, the mass, the structural sizing, and the trajectory. Nonetheless, this set of parameters is extremely time and resource-consuming: this is the need for surrogate modelling.

2.2 Software Setup

For this project, NASA uses three computational systems:

• INTegrated ROcket Sizing (INTROS): Based upon the vehicle setup, mass properties are established using an existing list of typical launch vehicle systems, subsystems, and propellants.
• Launch Vehicle Analysis (LVA): Provides quick turnaround preliminary structural design and analysis. The input is a list of parameters such as material properties, load factors, aerodynamic loading, stress, and stability. This analysis uses worst-case loads to determine the primary structural mass of a launch vehicle concept
• Program to Optimize Simulated Trajectories (POST): It uses a direct solution method to approximate the control function for an optimal trajectory

The input of INTROS is the following set of parameters*:

*For a full description of parameters, see original article

LVA is basically an extension of INTROS, so the two software are integrated in the following loop:

LVA computes the Gross Liftoff Weight (GLOW) and gets it back to INTROS until convergence is obtained.

POST uses the mass information from INTROS/LVA and computes the payload delievered.

2.3 NASA Surrogate Modelling

The first surrogate model goes from the parameters property to the mass information and mimics the behavior of INTROS/LVA. The output mass information coming from the first surrogate model gets input to the second surrogate model, which mimics the behavior of POST. The whole surrogate model looks like this:

The surrogate model algorithm that they used is extremely simple and it is known a Response Surface Equations (RSE).

Given that INTROS/LVA, and POST surrogate models can be run in a fraction of a second, we can run very large simulations and explore the dependency between the payload delivered and the parameters of the vehicle. The output is extremely helpful as it allows us to check the payload delivered based on multiple parameters:

For example, we can invert the dependency and find the necessary parameters to obtain the target payload delivered.

3. Conclusions

Thank you a lot for spending time with me. In this article, I tried to squeeze around 6 years of Python knowledge, 4 years of my doctorate (which is in Surrogate Modelling for Aerospace Engineering), and 2 weeks of paper studying, so I understand if some bits are a little bit confusing. Let me try to wrap up the key points for you:

1. Introduction to numerical simulation and Finite Element Methods (FEMs): We began by discussing the challenges of using computationally intensive numerical simulations, like FEM, for solving complex problems. These methods solve differential equations numerically and, while accurate, they take a lot of time and computational effort
2. Theoretical introduction to Surrogate Modeling: To address these challenges, we introduced surrogate models. These models replicate the results of more complex simulations but with significantly reduced computational requirements. Using surrogate models some unpractical studies become feasible, as the computational time is drastically reduced.
3. Hands on example on Surrogate Modelling: Using a toy example, I described how to implement a surrogate model, from Design of Experiment to Quality Assessment.
4. NASA Case Study. NASA uses surrogate models to provide mass information and payload delivered of a vehicle to third-party clients. We briefly described their public study.

4. About me!

Thank you again for your time. It means a lot ❤

My name is Piero Paialunga and I'm this guy here:

Image made by author

I am a Ph.D. candidate at the University of Cincinnati Aerospace Engineering Department and a Machine Learning Engineer for Gen Nine. I talk about AI, and Machine Learning in my blog posts and on Linkedin. If you liked the article and want to know more about machine learning and follow my studies you can:

A. Follow me on Linkedin, where I publish all my stories B. Subscribe to my newsletter. It will keep you updated about new stories and give you the chance to text me to receive all the corrections or doubts you may have. C. Become a referred member, so you won't have any "maximum number of stories for the month" and you can read whatever I (and thousands of other Machine Learning and Data Science top writers) write about the newest technology available. D. Want to work with me? Check my rates and projects on Upwork!

If you want to ask me questions or start a collaboration, leave a message here or on Linkedin:

[email protected]

Tags: Aerospace Artificial Intelligence Data Science Deep Dives Machine Learning

Comment