Hacking Causal Inference: Synthetic Control with ML approaches

The standard, presented in the literature and adopted at large scale by companies, to study the causal impacts of business actions (like design change, discount offers, and clinical trials) is for sure AB testing. When carrying out an AB test, we are doing a randomized experiment. In other words, we randomly split a population under our control (patients, users, customers) into two sets: a treatment and a control group. The treatment action is given to the treatment group, leaving the control group as is. After some time, we come back to registering the metrics of interest and analyzing the impact of treatment on population behaviors.
All that glitters is not gold! It's proved that AB testing suffers different drawbacks. The main assumptions behind randomized trials are:
- No interactions between the treatment and control groups (i.e. network effect).
- The increasing cost of large-scale experiments.
In the real world, the network effect is common since we may expect to register "contamination" among people. That's the case of opinion sharing across social media (in the case of a marketing trial) which influences each other choices. To override this inconvenience a solution consists in increasing the scale of the experiment by selecting people with different tastes across various geographical regions. Despite increasing the sample size may be a valid solution, it's infeasible since it increases costs exponentially. In this scenario, a technique called synthetic control was introduced.
In this post, we present the synthetic control methodologies for randomized experiment trials. The technique is introduced in this paper [1]. Our aim is not to show a mere implementation of the approach on a real-world dataset. We leverage the temporal dynamics present in the data to propose a variation of synthetic control using tools from the data scientist's arsenal.
WHAT'S SYNTHETIC CONTROL
Synthetic control aims to evaluate the effect of interventions in case studies. It's similar to any randomized experiment. In the preliminary phases, treatment and control groups are selected. Differently from standard causal analysis, the treatment population can assume any size!
Imagine being interested to verify the effectiveness of a treatment on a group composed exactly of a single unit. Adopting the classic synthetic control methodology, we end up building a weighted average of multiple control units to mimic the behavior of the treatment case (artificial control case).

Mathematically speaking, the problem consists in finding the optimal values of W (unit weights) that minimize the equation above. These values represent the contributions of each control unit in building the artificial control case.

We want to verify how the relationship between units changes before and after the treatment introduction date (intervention). If we notice a significative divergence between the artificial control case and the real treatment one in the testing period, we may affirm the treatment is successful.
SYNTHETIC CONTROL WITH PCA
Synthetic control is a revolutionary technique that provides researchers with rules for control case generation. By making the synthetic case looks like the treated case, it's possible to study the impact of any treatment actions over time.
What synthetic control does under the hood is to study the temporal dynamics of control and treatment units. Firstly, when building the artificial control case, the interactions between control units are studied. Secondly, the same interactions are extrapolated and verified after the treatment introduction. In other words, we are checking for relationship changes between units before and after the intervention.
In Machine Learning, we are used to checking for distributions and relations change over time. What if we apply a technique, usually used to detect relationship changes, in a causal context to verify the effectiveness of treatment experiments?
A good candidate for this task may be Principal Component Analysis (PCA). It's a well know technique adopted at scale in machine learning to solve various tasks. We decide to use it to learn the relationships of units before treatment introduction.
pca = make_pipeline(StandardScaler(), PCA(n_components=1))
pca.fit(df_train)Then we apply it to reconstruct the unit paths after treatment.
df_test_reconstruct = pca.steps[0][1].inverse_transform(
pca.steps[-1][1].inverse_transform(pca.transform(df_test))
)
df_test_reconstruct = pd.DataFrame(
df_test_reconstruct,
columns=df_test.columns, index=df_test.index
)In the end, we measure the reconstruction errors to quantify a possible change in each singular unit dynamic which may be due to treatment adoption.
reconstruct_errors = (df_test - df_test_reconstruct).mean()We apply the proposed methodology to study the restriction introduced by the state of California in 1988 (Proposition 99) on tobacco consumption. The amendment aimed to increase taxes on tobacco products to prevent the consumption of cigarettes.

The study is the same one proposed by Abadie in this work [2]. The data of the experiment are downloadable by everyone here and are released under a public license.
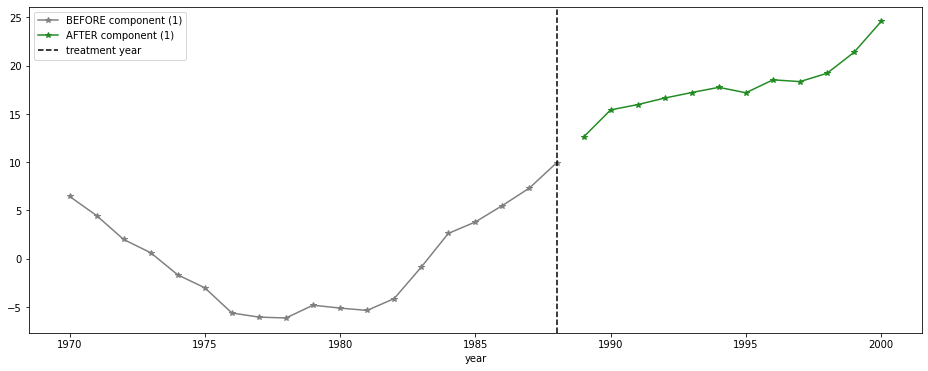
Analyzing the reconstruction error for each state independently, California registers the biggest negative reduction. For California state, we notice a significant deviation from the expected consumption (reconstructed by PCA) to the observed. This behavior may be due to an increase in tobacco taxes which leads to a reduction in cigarette consumption.

With a simple modeling strategy, we can learn the paths of various units under study. We can observe their expected behavior and analyze possible divergences from what we expect in normal conditions or with the introduction of treatment activities.
SUMMARY
In this post, we introduced synthetic control as a methodology to extract causal insights from the introduction of any treatment action. Classical synthetic control works by studying the relationships of units in the control group building an artificial control case. We discovered that it's possible to do the same in a straight forwarding way, simply studying the relationships between units and observing how they vary with time. We did it by analyzing the reconstruction errors of PCA after treatment introduction.
Keep in touch: Linkedin
REFERENCES
[1] A. Abadie, J. Gardeazabal, The Economic Costs of Conflict: A Case Study of the Basque Country (2003), The American Economic Review.
[2] A. Abadie, A. Diamond, J. Hainmueller, Synthetic Control Methods for Comparative Case Studies: Estimating the Effect of California's Tobacco Control Program (2010), Journal of the American Statistical Association.

