Hands-On Optimization Using Genetic Algorithms, with Python

Author:Murphy | View: 28887 | Time: 2025-03-22 20:17:57

Have you ever heard of this sales tactic?

"Are you tired of wasting hours during X? Why don't you try Y!"

I'm sure you did. For example: "Don't spend hours writing your own code, use our software instead!". Or "Stop wasting hours on your ads, use AI instead!" (my YouTube recommendation algorithm loves that one, and it's probably my fault because I'm always talking about AI).

This sales tactic is based on the fact that the time that you spend on a problem that you want to solve can be optimized.

"Nerdly" speaking, when you read this sales tactic, you usually have two options: exploration or exploitation. What do I mean by that? I'll explain in a moment. For now, remember the sales tactic, and put it in the back of your head. We'll be back on it.

Let's say you have a tool, a knob you can tune. By moving this knob, you get a waiting time. Imagine you are in line for a coffee at Starbucks and the knob has two states (0 and 1): 0 could mean "stay in the same line" and 1 could be "change the line". Which one means "waiting the least amount of time"? Should you change the line or be patient on the same one? I know you have had this problem at least once. I'm a big line changer, and my wife is a big line stayer.

Now, let's consider a knob that can move continuously, meaning you have infinite states between 0 and 1 (imagine a whole lot of "lines" if you will). Let's call this state x. Mathematically speaking, our problem has x (state) and y (waiting time):

Let's say we have states 0.2, 0.4, 0.6 and 0.8. For those states, we found the corresponding waiting times.

Now, given these 4 points, we have that the lowest waiting time is, let's say, at state x= 0.4. But are we sure that it is really the smallest amount of time? We don't know, but as we only have 4 points, it is highly unlikely that we found the smallest amount of time, especially considering that the area between 0.0 and 0.2 and the area between 0.8 and 1 are completely unexplored. What can we do?

We explore the other areas (between 0 and 0.2 and 0.8 and 1).
We exploit the areas where we think our minimum is going to be (between 0.2 and 0.6)

Do you remember the example of the sales tactic? This is equivalent to doing this:

We trust the sales guy, and we explore the unexplored area: we modify our previous behavior in order to see what happens in the unexplored part. For example, we buy the software they are trying to sell and give up with our coding.
We do not trust the sales guy and we exploit what we know: we dig in and refine our estimate. We do not buy their software and we improve our own coding skills.

Now, it would be nice to do both, right? It would be nice not to trust the sales guy 100% and trust ourselves 0%, but rather to explore and exploit at the same time. For example, you pay 20% of what he's telling you (for the hardest part that you don't want to deal with), and you do the dirty work you want to deal with by yourself, saving money.

Sometimes the situation is messy, and the story is more complicated than a guy trying to sell software: this is where Genetic Algorithms (GAs) come in. GA is an optimization method that is usually very good in considering both exploration and exploitation. The roots of Genetic Algorithms are in biology and I find this method extremely fascinating and powerful.

In this blogpost, we will do the following:

We will very briefly define the problem that Genetic Algorithms try to solve (optimization and global optimum)
We will describe the Genetic Algorithm from a theoretical point of view.
We will apply the Genetic Algorithm to a multiminima case.

Ok, a lot to cover. Ready? Let's get it started.

0. Optimization Idea

We did cover a little bit of the optimization idea in the introduction and there is no need to be super fancy with the math here. I'm just going to formalize the problem a little bit so that we will understand what we are talking about throughout the article.

Everything start with your parameters. Going back to the knob example, let's say you don't have only one knob, but you have multiple ones. Let's say you have k of them. Those are your parameters. Your parameters form a vector (or a list if you like computers), which is indicated with x:

For every x that you give me, I give you the corresponding loss (or cost). The loss is indicated with the letter L. The objective of the Genetic Algorithm is to minimize this loss, making it as small as possible.

Where X is your "space of solutions" represented by the whole boundaries for parameter 1, parameter 2,…, parameter k.

Good. That is as far as I'm going to get with the small talk. Let's talk about GA specifically now.

1. Genetic Algorithm Theory

1.1 Defining a population

Now, do you remember that I promised you that we were going to explore and exploit? The first thing to do to explore is to populate X with N elements. This will make sure that we start with an equal opportunity to "see" (or explore) everything without missing possible optimum "spots".

The idea of Genetic Algorithm comes from biology, so you will see a lot of biological terms. The original random sample is known as "Population". The Population will evolve throughout time (t), so we will define it as P(t). The Population has m elements, which are called chromosomes.

So this is our first population:

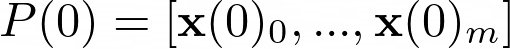
As we said, the elements of P(0) are randomly sampled from the k dimensional parameter space.

If you noticed that our parameter vector x became a function, it is because the vector will evolve with time as we look for the optimal solution

1.2 Selection process

So this is our first list of candidate. From this list, we can already see which one is better and which one is worse, right? For example, if m = 50, we might have L(x(0)_30)

This is our start. How do we improve? The first thing is to select the best ones (i.e. the ones that are more likely to be the minimum). The "best ones" in math mean "the ones that maximize the fitness function". In the case of minimization, the fitness function is defined as f(x) = -L(x).

So again, at time 0, the fitness function will give us the following values:

Now, how do we select "the best ones" using this fitness function? We could just do "the one with the largest fitness values", which is very intuitive. Nonetheless, one of the best ways to do that is by doing the "roulette selection" which means extracting them with a probability that is proportional to the fitness function. This means that the probability of extracting the ith chromosome is, at time t=0:

This method is robust: if you only have 1 chromosome, the probability is 1 because you don't have any other choice.

So, based on the probability defined above, we start selecting kchromosomes, which we will call parents for reasons you will know in a second. These parents are randomly picked, but they are most likely elements with good fitness values because of how we defined the probability.

1.3 Parents And Children

Now, Genetic Algorithms are part of evolutionary algorithms, meaning that step t is the evolution (improvement, if you may) of step t-1. So how do we evolve? Unfortunately, it's not like Pokémon, you actually need at least two "parents" to generate a "child" also known as the "offspring". The "parents" candidates are the k candidates that we selected, for example, using the roulette selection described above. You need to generate the same amount of offsprings as the original population (m).

You can select the couple of parents in multiple ways. You could take them all randomly, or start with the first parent and "pair" it with all the other parents. Then do it with the second parent and "pair" with the remaining other parents, and keep doing this until you reach number "m" offsprings.

But how do we combine two parents? We do so by applying a technique called crossover. We select the index k, then we mix the two starting from that index, just like you see in this scheme below:

This idea has two principles:

Trying to get the best out of both parents: we are aiming to get the qualities that make parent P a good fitness chromosome and the qualities that make parent Q a good fitness chromosome and mixing them.
Explore new region: geometrically speaking, by doing so you are actively exploring new areas.

This is the core of exploration vs exploitation, and that is why evolutionary methods are historically known to have a good tradeoff of these two wanted effects.

By doing so m times we will have m offsprings. These offsprings are the new population and we'll call this new set of offsprings at time t:

So, let's recap what we did so far:

We selected our sample randomly
We sampled a list of parents candidates using the fitness function as a probability indicator
We selected the parents from the list of candidates and paired them
We generated an offspring from each pair, thus enhancing the exploration and exploitation of the minima.

Beautiful. We are almost there, I promise.

1.4 Mutation

Now the next step is to mutate our offsprings. What I mean by that is that we want to add some sort of randomness, meaning that we don't necessarily want x(t) to be just a mix of x(t-1) but we want it to be different. If you think about it, in life, you are not just the result of a genetic mix up but you are also the result of randomness: how things that happen around you change you.

Philosophy aside, this is how you add mutation:

This allows you to explore different realizations of xs but, at the same time, you are also exploiting the surroundings of your best maximum (or minimum). Remember that this will give us m elements, because X(t) is a matrix with m rows, so your population is ready for step t+1.

1.5 Stopping Criterion

When do we stop this process? There are multiple ways to do so. The first method is just to set the number of iterations. For example, tmax = 10: after 10 refinements, you stop (at P(10)). Or you can consider the fitness as a reference: when the fitness doesn't increase enough from time t and time t+1 or_ when it reaches a certain threshold, you stop optimizing. Whatever your criterion is:

If the criterion is not met, you redo step 1.2–1.4
If the criterion is met, you stop.

2. Genetic Algorithm implementation

Now, this process is fairly simple in practice: select the population randomly, improve it by crossover and mutation, stop if your stopping criterion is met.

Surprisingly, it is even simpler to implement it in practice. Let's see it step by step.

2.1 The library

PyGAD is a library that gives you full control of the parameters (population size, number of parents, stopping criterion and much more), but it is also extremely easy to use. Let me be fair: the math of Genetic Algorithms is not complicated and you could develop it from scratch using object-oriented programming. Nonetheless, for the sake of simplicity and efficiency we'll use the PyGAD implementation.

Let's install it using:

pip install pygad

This library offers very cool integrations too, for example, they train Neural Networks using GA, which is very interesting.

2.2 The parameters

Tuning Genetic Algorithms based on your best need (the so called hyperparameter tuning process) is an art itself. There are so many things that you could change to find a minimum that is lower than the minimum you just found and improve your results. The list of all the possible parameters can be found in here. Let me just give you an idea:

fitness_func and gene_space: they are super important as they are the fitness function (what you define as "best solution") and the boundaries of the space you are looking for
keep_parents: is a cool one, it gives you the option to keep the parents in population P(t+1), so you don't only have the offsprings, but you keep the parents as well for next iteration.
parent_selection_type: there are multiple ways to select the parents out of a population. Above, we described the "roulette wheel selection" but there are methods like "steady-state selection" or "stochastic universal selection" too. This parameter allows you to modify the method
mutation_type: There are multiple ways to "mutate" your population. We discussed "random" but there is also "swap" or "inversion".
crossover_type: There are also multiple ways to do the "crossover" operation. We described the "single point" (we called it k) but you can also apply "two-point", or "uniform" crossover strategies for combining genes.

Again, this is far from being the full list as there are so many parameters you can tune. But this is a good thing! Tuning the parameters is how you tune your GA to find the best optimum and converge to the global optimum.

2.3 The code

This whole story can be summarized in a single block of code. I'm going to give you the code and then we are going to discuss it.

This is what we did:

Defined our fitness function, that is "minus the function we are trying to optimize". If the function you are trying to optimize is a black box (maybe it comes from a complex model or something), the fitness is still minus that function by definition
Set the parameters, like "m" (population size), "num_generations" (how many refinements of loop you do) or "num_genes" that is the dimensionality of your input.
We gave all these parameters as input to the GA instance.
We run the optimization by doing ga_instance.run()

2.3 The application

I don't want to focus on the results too much, but just for the sake of showing you that this works, I'm going to show you how they look like. If you run the previous code successfully, the ga_instance.solutions will be a kD x N matrix, where:

k is the dimensionality of the input
N is the number of iterations

We can plot this matrix to keep track of how our Genetic Algorithm is optimizing our function:

In this example, we were trying to minimize a bizarre function of x and y in 2D and we can see how the GA is correctly guessing the minimum area (even with multiple local minima).

But again, the point of this blogpost is to describe how to use GA and how to use PyGAD for your own optimization task, so absolutely do feel free of changing the fitness/loss function and all the other parameters.