How To Forecast With Moving Average Models

Background
In my previous post we covered autoregression. This is where you forecast future values using some linear weighted combination of previous observed values of that time series. Rather than using the previous observations, we can forecast using past forecast errors instead. This is known as the _moving-average (MA)_ model.
This is not to be confused with the rolling mean model, which is also dubbed as a moving average model.
In this post I want to go over the theory and framework behind the moving average forecasting model and then dive into a short tutorial on how you can implement it in Python!
Moving Average Model Theory
Overview
As declared above, the moving average model is regression-like by fitting coefficients, θ, to the previously forecasted errors, ε, also known as _white noise error, with the additon of a constant term that is the mean, μ_:

This is a MA(q) model, **** where **** q is the number of error terms, which is known as the order.
Requirements
One key requirement of the MA(q) model is that, like autoregression, it needs the data to be stationary. This is means it has a constant variance and mean through time. This can be achieved through differencing and stabilising the variance through a Logarithm or Box-Cox transform.
If you want to learn more about stationarity and these transformations, checkout my previous articles on these subjects below:
Order Selection
Selecting the order of a MA model can be accomplished by viewing the autocorrelation function. Autocorrelation measures the correlation of the time series at various time steps (lags). If a lag has a high correlation, then it is influential in describing what the current value of the time series is. This idea of ‘influence' can be used to carry out forecasts.
We can use autocorrelation to plot a correlogram of the various lags of the time series to determine which are statistically significant in impacting the forecasts. If this is hard to visualise at the moment, don't worry we will carry out a Python tutorial on this exact process later!
If you want to understand more about autocorrelation, checkout my previous article on it here:
However, another more common approach is to simply iterate over different combinations/number of orders and use the model that gives the optimal performance. The optimal performance is typically evaluated by the model that returns the best _Akaike information criterion (AIC) value, that is based on maximum likelihood estimation. This process is analogous to hyperparameter tuning_ in classical Machine Learning.
Estimation
Now that we have our order of MA terms, we need to fit their coefficients! Unfortunately, this is not as easy as in linear or autoregression as the errors are not observable. So, how do we do it?
Well, it is not so straightforward and I will leave a link here for a full mathematical walkthrough which explains this process well. However, the general gist is that the autocorrelation values for each lag are directly related to their coefficients. Therefore, once you know the autocorrelation of a forecast error, you can work backwards to acquire its coefficient.
For example, for a MA(1) model (model with one forecast error term), its autocorrelation, _c_1_, is:
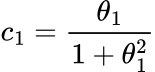
One can see that if we know _c_1, then this is just a simple quadratic equation that we can solve for the coefficient. This same idea can be extended to a MA(q)_ model, but with more complexity of course due to multiple errors and coefficients.
Python Tutorial
Let's now implement the moving average model in Python!
Data from Kaggle with a CC0 licence.
Data
First plot the data:

Clearly the time series has a yearly seasonality and a consistent upward trend. Therefore, we need to make it stationary through differencing and the Box-Cox transform:

The data now appears to be stationary. We could have made it further stationary by carrying out second order differencing or seasonal differencing, however I think it is satisfactory here.
If you want to learn more about these more sophisticated differencing methods, checkout my previous blog post here:
Model
We can now start the modelling phase by finding the optimal number of orders. To do this, we plot an autocorrelation correlogram like we discussed above:

The blue region signifies where the values are no longer statistically significant. From the above plot, we can that see that the last significant lag is the 13th. Therefore, our model order for the MA model will be 13.
Unfortunately, no direct MA model function or package exists in Python, so we are going to use the _ARIMA_ function from statsmodels and set every component to zero apart from the moving average orders.
Don't worry about what ARIMA is or stands for, I will cover it in my next article!
Analysis
Let's now plot the forecast by undifferencing the data and carrying out the inverse Box-Cox transform:

We can see the forecasts have captured the trend mostly well, however they have failed to notice the seasonality. In my previous article, the autoregression model, that was trained on the same data, managed to pick up both the trend and seasonality. You can checkout the autoregression modelling walkthrough here:
Summary and Further Thoughts
In this article, we have learned how to forecast with the moving-average model. This is where you forecast future values as a linear combination of the previous forecast errors. It is easy to implement in Python, however didn't lead to as good results compared to the autoregression model we saw in my previous post.
Full code used in this article can be found at my GitHub here:
Medium-Articles/moving_average.py at main · egorhowell/Medium-Articles
Another Thing!
I have a free newsletter, Dishing the Data, where I share weekly tips for becoming a better Data Scientist. There is no "fluff" or "clickbait," just pure actionable insights from a practicing Data Scientist.
Connect With Me!
References and Further Reading
- Forecasting: Principles and Practice: https://otexts.com/fpp2/

