No Label Left Behind: Alternative Encodings for Hierarchical Categoricals

Author:Murphy | View: 28437 | Time: 2025-03-22 21:41:48

In my work as a data scientist, I see a lot of labels. Data contains zip code labels, gender labels, medical diagnosis labels, job title labels, stock ticker labels, you name it. Labels may be simple (shirt sizes of S,M, L) or complex (The International Classification of Diseases system encodes over 70,000 medical conditions, which can be hilariously specific).

When they occur in data, we call labels categorical features. Categorical features that have "a lot of" possible values are high-cardinality categorical features. High-cardinality categoricals present difficulties when used in machine learning models. A high number of dimensions makes them impossible or impractical to use directly (e.g. the "curse of dimensionality"). Therefore, various Encoding schemes are used to simplify these features.

Low-frequency or unseen codes also offer challenges for high-cardinality categoricals. For example, some zip codes are sparsely populated, while others contain millions of people; we are more confident of encodings for some. In addition, common code sets, like medical diagnosis codes are updated periodically, leading to unseen values not available to training. Unseen and low-volume codes can be important for growing businesses or products, or when training data is limited.

Encodings must account for low-frequency and unseen values in a way that preserves response information while resisting overfitting. In standard target encodings used in tree-based models, this is done by blending the overall mean with sample means in a manner proportional to counts.

Encodings must account for low-frequency and unseen values in a way that preserves response information while resisting overfitting.

Some high-cardinality categoricals can be organized into groups. For example, zip codes could be (roughly) aggregated to counties, states, or regions.

Group information might help us predict low-volume or unseen codes. It is possible to incorporate this information into target encoding using hierarchical blending of higher-level group means [1–2]. I tried this in my last blog post and saw increased performance on unseen codes, but over-fitting for some groupings [3].

Since then, I've been wondering about alternative treatments for hierarchical categoricals. Is it better engineer a feature to contain as much information as possible about a code system, or to find a way to let a model do the work?

Here, I test alternatives to hierarchical blending in an Xgboost model. I see some performance improvements when separate fields are used for hierarchy levels, as opposed to blending them into a single feature. Simple thresholding, where low-volume codes are set to null (or another value indicating uncertainty), seems especially resistant to over-fitting. Hierachical blending has a slight advantage for the standard code hierarchy, but overfits badly for some code groupings.

Shapley tests show that multi-feature encodings allow the model to leverage information from higher levels of a categorical hierarchy and from other predictors.

Thresholding is like opening a window to allow other sources of information to shine through.

A major caveat is that a model needs to be trained on low-volume cases to generalize to unseen cases. This applies to most variants of target encoding I examine, excepting hierarchical encoding. In addition, all encoding methods discussed in this post probably have bias risk if low-volume or missing codes are unlike unseen codes.

Therefore, I wonder if random injection of null (or other) values into training data could help teach a model how to generalize to unknown codes. I tested something similar for entity embeddings in neural networks, and saw a substantial performance boost for unseen codes [3]. Maybe a similar strategy might be help XGBoost. It would be nicest if randomization could be shuffled in training iterations/epochs.

Methods

I use XGBoost binary classification models to predict loan defaults among establishments in the U.S. Small Business Administration (SBA) Loans dataset [4–5]. This is a public dataset (CC BY 4.0). Methods are mostly described previously [3]. All code is available in GitHub [6].

I encode the NAICS (industry feature). NAICS codes have an official, 5-level hierarchy, which groups establishment types into buckets of varying granularity [7]. See Table 1 for examples:

**Table 1:** Examples of the hierarchical organization of North American Industry Classification System (NAICS) codes [7]. The 6-digit NAICS (National Industry) grouping is the most specific (or "lowest") level of the hierarchy, and these codes are grouped into more general (or "higher") levels. The triangle at the right represents the higher number of codes at lower levels of the hierarchy. Image by author.

One important difference from previous methods is I sometimes use a different value (100) of the blending midpoint. This is done to help compare performance to new methods that are more sensitive to the midpoint. Result are very similar, but not identical, to those in [3].

Exploring Alternative Encodings

Here's are the encoding variations I am going to try:

Target Encoding (NAICS only): Standard target encoding of the NAICS feature only (1 feature)
Hierarchical Blending: Target encoding that blends higher-level group means into the observed rates to better estimate the response (1 feature)
Target Encoding (all): Standard target encoding of all levels of the NAICS hierarchy (5 features)
Target+Count Encoding: Same as 4, but include additional count encoding features (10 features)
Target-Thresh Encoding: Like standard target encoding, but instead of shrinking low-volume/unseen values towards the target (or any) mean, just set values below a cutoff point to null. (5 features)

For all the above, the encoding of the lowest-level NAICS feature is very similar; they're actually identical for 1, 3, and 4. For 2 and 4, variations only occur in lower volume or unseen codes. Methods 3–5 involve additional features beyond encoding the lowest-level code.

Target Encoding (NAICS only): Standard target encoding replaces a categorical feature with the mean response (loan default rate) for a given category. The mean is calculated on the training data, to avoid leakage.

The mean estimate is obviously not very reliable for low-volume codes, leading to overfitting risk. Therefore, target encoding usually involves blending the overall target data mean into the encoding, so that very low volume (or unseen) codes get values like the target mean, while higher volume codes are mapped to nearly their actual response. The meaning of "low volume" depends on target rate, and so the blending is parameterized. Here, I use a sigmoidal function parameterized by the blending midpoint and width (I vary midpoint in some tests).

Hierarchical Blending: Hierarchical blending is a variation of target encoding, where higher-level NAICS group means are used to get a better estimate of the mean response for low-volume or unseen codes [1–2]. The response is blended with means from all available levels of the hierarchy, using the same sigmoidal function to weight each level.

Target Encoding (All): This method is the same as target encoding (NAICS only) but you also target encode higher level codes, e.g. NAICS sector or industry group, for 5 total features.

It makes some sense that a nonlinear model might "automatically" incorporate the higher-level features when needed. On the other hand, for most codes, higher-level group features will not offer additional information.

Target+Count Encoding: I wondered whether XGBoost might be able to leverage count information to infer that a target encoded feature is not reliable for low-volume or unseen codes. So, I am trying a "Target+Count" encoding, which just adds count encoding features to Target Encoding (all), for a total of 10 features. I threshold count encodings above a certain level, which corresponds to point where the fraction of response is 95% or more due to the sample mean (< 5% "blended")

Target-Thresh Encoding: If a nonlinear model might use count information to modify its response to a feature, maybe it can get similar information from missing values, or a specific value. What if I just told the model that "I don't know" the mean of low-volume codes, and let it sort itself out? Target-Thresh encoding is the same as target encoding for higher volume codes, but for lower-volume or unseen codes, values are set to null.

So, how do they perform?

I do a usual randomized train/validation/test split, but also set aside a sample of 10% of NAICS codes to assess performance on unseen values (see [3] for details). I report the precision-recall area under the curve (PR-AUC) metric, as this emphasizes detections of defaults (higher values are better).

**Figure 1.** XGBoost model performances with different NAICS encodings as a function of the blending midpoint (or count threshold for target-thresh encoding). The left panel shows PR-AUC for the random test dataset, the right panel PR-AUC for the holdout NAICS test dataset. Image by author.

Test Data

The left panel of Figure 1 shows performance on the test dataset. Standard target encoding and hierarchical blending are very similar for most midpoints. However, all three multi-variable encoding methods (target encoding (all), target+count and target-thresh) show a slight but meaningful performance boost. These three curves are very similar to each other.

For all the encodings, performance degrades at very high midpoints, which is expected as information about mean responses is being lost (note the overall target rate is about 20%). The degradation is worst for standard target encoding, which includes no information from the code hierarchy.

If I was to look only at the left panel of Figure 1B, I might conclude that one of the multi-field encodings is best. But what about unseen codes?

Holdout Data

The right panel of Figure 1 shows performance on unseen NAICS codes. Values tend to be lower than the left panel, as expected for unseen codes, whose mean response are not available to training.

Target encoding (NAICS only), the only method to completely ignore the NAICS hierarchy, has the worst performance. Now, hierarchical blending appears strongest, and does not seem as sensitive to blending midpoint as the multi-feature methods. The multi-field encodings seem to improve about a midpoint of ~100. I'll discuss this later.

If I look at the Figure 1 right panel results, I might conclude that hierarchical blending would be preferred when unseen codes are important. However, in my previous post [3], I saw that hierarchical blending ran into overfitting trouble for some code groupings. So, I have more testing to do.

What about different code hierarchies?

NAICS has a standard hierarchy which is in widespread use. But, what about other codes which might have different arrangements? Maybe different numbers of levels, or different granularity, will make a difference. In all hierarchy tests, I fix the blending midpoint/threshold at 100.

NAICS standard hierarchy variations

To get an idea how models might respond to hierarchy variations, I use the same encoding methods, but start at different points in the NAICS hierarchy. Rather than use all 5 levels, I would use the base NAICS, and then groupings from, say, the 3rd level and up. Figure 2 shows performance when the starting point is changed in the standard NAICS hierarchy.

**Figure 2.** XGBoost model performances for NAICS encodings that use different portions of the standard NAICS code hierarchy. Blending or feature addition starts at or above the level shown. The k values on the x-axes are the number of distinct codes in each level. The left panel shows PR-AUC for the random test dataset, the right panel PR-AUC for the holdout NAICS test dataset. The baselines from standard target encoding are horizontal gray lines on both panels. Image by author.

For the random test dataset (left panel), Figure 2 results are very similar to Figure 1, with Hierarchical Blending being pretty like standard target encoding, but the multi-field encoding methods increasing performance. This pattern occurs regardless of the level from which encoding is done.

The right panel of Figure 2 shows that performance on unseen codes varies strongly as the hierarchy changes. For hierarchical blending, using only the highest-level group (sector) for blending actually results in worse performance than simple target encoding (this result was also seen previously [3]).

DGI feature-based groupings

In addition to modifying the standard NAICS hierarchy, I'll try some completely different code groupings. In my last post [3], I tried Deep Graph Infomax (DGI) plus clustering to create groups based on predictor fields. DGI groups are correlated with model response, but don't contain additional information above the predictor fields.

Previously, DGI groups led to overfitting for hierarchical blending, suggesting that method may be risky, especially when groupings risks are redundant with other predictors [3]. How do other methods respond to DGI groupings?

**Figure 3.** XGBoost model performances for NAICS encodings that use a code hierarchy based on DGI groupings. Blending or feature creation starts at or above the level shown. k values on the x-axes are the number of distinct codes in each level (values are chosen to match the standard NAICS groups in this dataset). The left panel shows PR-AUC for the random test dataset, the right panel PR-AUC for the holdout NAICS test dataset. The baselines from standard target encoding are horizontal gray lines on both panels. Image by author.

Figure 3 shows DGI groups often lead to performance degradation due to overfitting. This is worst for target encoding (all) and target+count encoding. Hierarchical blending overfits for some hierarchy levels, but not others. Target-thresh seems to resist overfitting for DGI groups.

Totally random groups

Given overfitting with DGI groupings, I wondered what might happen with random groups.

Random groups simulate a case where the code structure doesn't relate to a problem. Code systems are often maintanined by government or industry experts for their own purposes, which may not relate to your outcome of interest. For example, imagine if a we used a hierarchy that organized industries alphabetically in this loan default model.

**Figure 4.** XGBoost model performances for NAICS encodings that use a code hierarchy determined at random. Blending or feature creation starts at or above the level shown. k values on the x-axes are the number of distinct codes in each level. The left panel shows PR-AUC for the random test dataset, the right panel PR-AUC for the holdout NAICS test dataset. The baselines from standard target encoding are horizontal gray lines on both panels. Image by author.

Figure 4 shows results from groups created entirely at random. Most of the encoding methods do nothing with the hierarchy, which is reassuring. However, hierarchical blending overfits quite badly!

Feature Importances

Shapley tests can provide some drill-down information about how different encoding methods affect predictions. In Figure 5, individual SHAP values, which reflect a feature's contribution to a prediction, are aggregated, to show overall responses for specific test cases.

There is a lot going on in Figure 5 but start with the blue bars, which represent "other" (non-NAICS related) predictors. These are longer in the right column of plots, compared to the left. For unseen codes, models increase their reliance on features other than NAICS encodings. This effect is strongest the multi-feature methods (target encoding (all), target+count encoding, and target-thresh encoding).

The orange bars show the importance of the encoding of the low-level NAICS code. Differences are small in the test data, but for the holdout data, hierarchical blending stands out. That high reliance on this feature is consistent with the overfitting seen above.

Target encoding is just a simple model to predict loan defaults based on NAICS alone; these predictions are then fed into XGBoost. Hierarchical blending is a more complex precursor model. It appears that there is a bias-variance tradeoff here, and hierarchical blending overfits.

It seems better to admit ignorance than to guesstimate the mean.

Finally, the green bars show importances for features derived from higher levels of the hierarchy (or counts); these exist only for multi-feature methods. Higher-level effects are strongest for the standard NAICS hierarchy (2nd row of plots). The standard hierarchy provides extra information to the model, whereas DGI and random encodings add little or no value.

Simpler encoding methods allow the primary feature to step back. Instead of over-relying on a feature when we have incomplete information, we let the model find alternative sources.

What about missing values?

I think that the composition of the training data, in terms of both low-volume and missing codes, are crucial considerations.

Target-thresh encoding works for this dataset, and maybe would be fine in other contexts, but there are scenarios where I believe it would fail.

My dataset has no missing values. The original data had nulls, mostly for older (pre-2000) loans, so I dropped those cases [3]. Those long-term loans mostly have low default rates.

I think sporadic missing values not correlated with the outcome would help the model learn what to do with unknowns. But in this dataset, there is likely to be a bias in the unknown values as they reflect loan age. Then, if target+thresh used nulls for unseen codes, I might expect poor performance, especially as there would probably be more rows with missing values vs. low-volume codes.

In the absence of missing values in training data, target encodings depend on low-volume codes to generalize to unseen labels. Remember Figure 1, where performance of the multi-field methods on unseen codes rose at ~100? I usually think of the ideal midpoint for target encoding as depending mostly on the target rate. Instead, for Figure 1, I think the midpoint depends more on having enough low-volume cases for training. Returning to the window metaphor – that window needs to be open enough. I need enough examples representative of uncertain rates for the model to learn to rely on other features.

In the absence of missing values in training data, target encodings depend on low-volume codes to generalize to unseen labels.

In Figure 1, I also see that there is a tension between having a high enough midpoint to generalize to unseen codes, and too high a midpoint resulting in lost information. I have a good amount of data, and NAICS are unevenly distributed, so there is a range that works. Would this always be the case? Are there datasets with no right balance?

In the plot below, I do the exact same encodings as Figure 1, but then remove low-volume codes from the training data before the XGBoost fit:

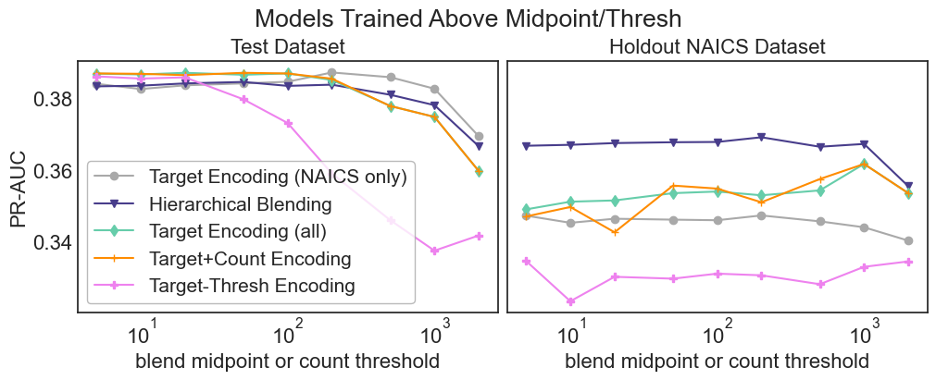
**Figure 6.** Like figure 1, but low-volume cases removed prior to train. The encoding threshold is varied (x axis). he left panel shows PR-AUC for the random test dataset, the right panel PR-AUC for the holdout NAICS test dataset. The baselines from standard target encoding are horizontal gray lines on both panels. Image by author.

Figure 6 shows that target+thresh performs poorly when the training data doesn't have any nulls. When I use target+thresh but fill with the training data mean for the scenario in Figure 6, target+thresh performs very similar to target encoding (all) and target+count (not shown).

Figure 6 also shows that hierarchical blending results are unaffected by changes in the training data prior to the fit. All of the information about the hierarchy means is contained in the encoded feature. But the other methods rely on the model learning to compensate for low-volume or missing codes.

I am wary of how dependent results are on the characteristics of low volume and unseen cases in the training data. I think that some sort of randomization – setting training values to missing or the target mean – might help. With randomized missing cases, bias might be reduced, and I could be sure I had enough relevant training examples. The downside of such randomization is information loss, and so it might be nice to randomize during training, maybe setting different observations to null at each boosting round.

What about other model types?

I tested XGBoost and would guess that results would extend to other boosted tree models. For models that don't allow missing / null values, target-thresh would need to use a constant value fill; I did several tests with this, and it seems fine. In fact, figure 6 shows that a constant fill may be preferred if the training data has few low-volume codes. But, I wonder if it might still be problematic in certain cases, e.g. if default rates for some codes are similar to the overall mean.

For multi-feature encodings, random forest models would probably leverage higher-level group features to a greater extent (column sampling in XGBoost might have a similar effect). This would impact all observations but might be helpful for low-volume or unseen codes.

Target encoding is often used in tree-based models, but analogous concerns apply for entity embeddings in neural network models. Previously, I found that neural network models overfit badly unless I randomly set training data inputs to the code used for unseen cases [3]. I suggested that randomization to some students, who also saw a big reduction in overfitting. So, for N=2 examples, randomization helps entity embeddings generalize; maybe it's a promising strategy.

Final Thoughts

As someone who makes her living building models that rely on high-cardinality categoricals, what I'd like is an easy-to-use system that gives good performance for both seen and unseen codes, with low overfitting risk. I don't feel like I'm quite there with any of the methods I've tested yet, but maybe some are getting close.

Maybe a convenient system would involve target-thresh encoding, with some sort of fitting to determine the optimal threshold (analogous to scikit-learn's TargetEncoder [8]). I'd also need some sort of randomized nullification/fill, so models can learn from higher level features whether or not there are (enough) low-volume codes in the training data, and even when pre-existing missing values reflect data biases. For ease of use, it would be nicest if nullification was built into model training; shuffling data would also reduce information loss.

I hope to explore these ideas more in future posts! I would love to hear suggestions in the comments. What do you do with your categorical features? What problems have you seen?