The stacking ensemble method
Discover the power of stacking in Machine Learning – a technique that combines multiple models into a single powerhouse predictor. This article explores stacking from its basics to advanced techniques, unveiling how it blends the strengths of diverse models for enhanced accuracy. Whether you're new to stacking or seeking optimization strategies, this guide offers practical insights and tips to elevate your predictive modeling game with scikit-learn.
While this article is based on scikit-learn, I provide at the end a pure Python class that implements and mimics the stacking models of scikit-learn. Reviewing this pure Python implementation is an excellent way to confront and test your understanding.
In this post, we'll see:
- how stacking is part of ensemble techniques in ML
- how stacking works internally to provide predictions
- how it is fitted
- what is "restacking"
- how multi-layer stack can be created
- how and why we should inspect the performance of the base models
- how to tune and optimize the use of stack models

If you like or want to learn machine learning with scikit-learn, check out my tutorial series on this amazing package:
All images by author.
Stacking as an ensemble technique
Stacking is an ensemble technique in machine learning, meaning it combines several "base-models" into a single "super-model". Many different ensemble techniques exist and are part of some of the best performing techniques in traditional machine learning.
By "base-models", I mean any traditional model you might have encountered – those you can import, fit, and predict directly from scikit-learn. Those base models are for example:
- linear regression or logistic regression (and their variants like LASSO or Ridge)
- support vector regressor or classifier
- decision tree regressor or classifier
- K-Nearest Neighbors regressor or classifier
Individually, all these models have their own pros and cons, their own hyperparameters, their own zone of ‘comfort'. Hence, they might perform differently on your ML problem: they can have a different score overall your dataset, as well as perform better for some samples/zones in the dataset, and worst elsewhere.
The general idea of ensemble methods is to combine several such base models into a single better one. For the stacking techniques, we'll use those models as the buiding bricks, as well as our mean of combining the predictions.
Let's review quickly some common ensemble model techniques:
- voting: a voting ensemble is created from a set of base models, and the final prediction is computed simply by averaging the predictions of the base models (for regression) or the most-predicted class (for classification). This is one of the simplest ensemble technique (and easiest to understand/explain).
- boosting: the predictions of a series of weak learners (almost dummy models) are adjusted recursively using weights. This technique led to the Adaboost algorithm and GradientBoosting, and are among the top performing turnkey models.
- bagging: aka boostrap-aggregating: a parallel ensemble technique where many individual models are fitted on different subset of the whole dataset. The prediction of all these models are then combined (using a voting/averaging). When the individual models are decision trees, this technique leads to random forest algorithms.
- stacking: this is the ensemble technique this post explains, just keep reading!
So stacking is just one option among the ensemble techniques. As we'll see, stacking differs from the above ensemble techniques in many ways:
- it does not combine the base models in a sequential way
- it does not update the weighting of a model in a recursive way
- it does not simply average the predictions of the base model
- it works with a collection of various kinds of models (LinReg, KNN, SVM, etc) whereas bagging and boosting usually use a collection of the same base model (usually decision trees)
How stacking works
One of the biggest differences and specificities of the stacking method is how the base models are structured and the final predictions are computed. The structure of a stacking ensemble is the following:
- a set of base models constitute the ensemble: they are fitted and predict independently. These models are also called the "base layer", or "layer 0" of the stack structure, similarly to a voting ensemble. Those base models might be called "weak learners" as they are in boosting/bagging context, but note that they are not weak learners strictly speaking.
- another single model will wrap the predictions of the base models and compute the final predictions. This model is also called "final layer", or "layer 1"
Schematically, it'd look like this (we focus on the predicting process for now):

The important thing that makes the specificity of stacking is the following: internally, the final model of the stack does not work with the usual input dataset X, but instead learns/predict from the predictions of the base models. The idea is to use a model to fit/learn how the base models predict the output y, compare those predictions to the actual true y_true.
After the model has been fit, the predict process is simply the following: for a new X dataset (X or even a single sample x):
- all base model predictions are computed, independently: for model in base_models:
y_pred=model.predict(X) - all these
y_predvectors are concatenated horizontally, so to create a new 2D dataset, where each column represents the predictions for a given base model, we'll call this matrixX_finalbecause it represents the 2D input dataset of the final estimator - this
X_final2D dataset is used by the final estimator to predict the actual, final prediction:final.predict(X_final)

Put differently, there is an intermediate 2D dataset matrix that is created internally, composed of the y-predictions of the base models, and this matrix is used as the input for the final model – meaning the final model takes a 2D matrix of y-space values, and output the actual 1D prediction of y-space values.
Another way to see stacking is as a voting model, except instead of simply taking the average/most-voted prediction, we feed those predictions to another model. Put differently, we could mimic voting with stacking by using a plain averaging/argmax model as the final model.
Usually, the final model used is a simple LinearRegression for regression problems and LogisticRegression of classification problems, and those are the defaults of scikit-learn StackingClassifier and StackingRegressor. The step of combining the base models predictions by the final estimator is sometimes called "blending" as all the models predictions are blended into a single prediction.
Fitting a stack model the right way
The specific way a stack model works makes it necessary to use a specific fitting procedure.
As with any estimator, this is done automatically behind the scene by scikit-learn – so you don't absolutely need to understand this fitting procedure to use a stack model. On the other hand, it is always a good thing to understand how your models work – and it is super fun and gratifying to learn new things!
The algorithm used to fit a stack can be decomposed into 2 steps. The first one is pretty simple, while the second one needs a bit more explanation:
- step 1: all base models (those from layer 0) are fitted completely independently and using the whole X/y dataset. In other words, the first step is equivalent to:
for model in base_models: model.fit(X,y) - step 2: the final estimator is fitted using a cross-validation scheme with unfitted base models
The first step is pretty self-explanatory: when the fit method is called on the stack model stack.fit(X,y), the X and y are handled to each of the base models and they are fitted independently from each other. This step is equivalent to for model in base_models: model.fit(X,y). Those fitted estimators are stored in the stack.estimators_ attribute of the stack model.

Then in order to train the final estimator, a different approach is used. We already have the target output y for that fitting, but we still need to generate the intermediate X_final dataset created by the predictions of the base models. Using the .predict method on the already fitted estimators would lead to some kind of overfitting since the input X has already been seen and trained on by the base estimators.

In other words, we cannot use the already trained base estimators to feed the input dataset to fit the final estimator. Instead, each estimator is fed with the same cross-validation fold to the cross_val_predict function to generate a y_pred for all the base estimators. Those base predictions are then horizontally concatenated in an X_final training dataset so the final estimator fits with final_model.fit(X_final, y).

Now we know to decompose the problem as: "the X dataset the final estimator uses to fit on the target y is created by concatenating the predicted values by all estimators given by the cross_val_predict function" (using the same cv strategy for all estimators, in order to account for the fact that all base estimators always see the same input/output). This means that the fitted base models from the first step (those fitted with the whole X dataset) are not used to fit the final estimator. Instead, a copy of the unfitted base models are used for each fold, and the predictions for each folds are concatenated (vertically for each model, and horizontally to create X_final).
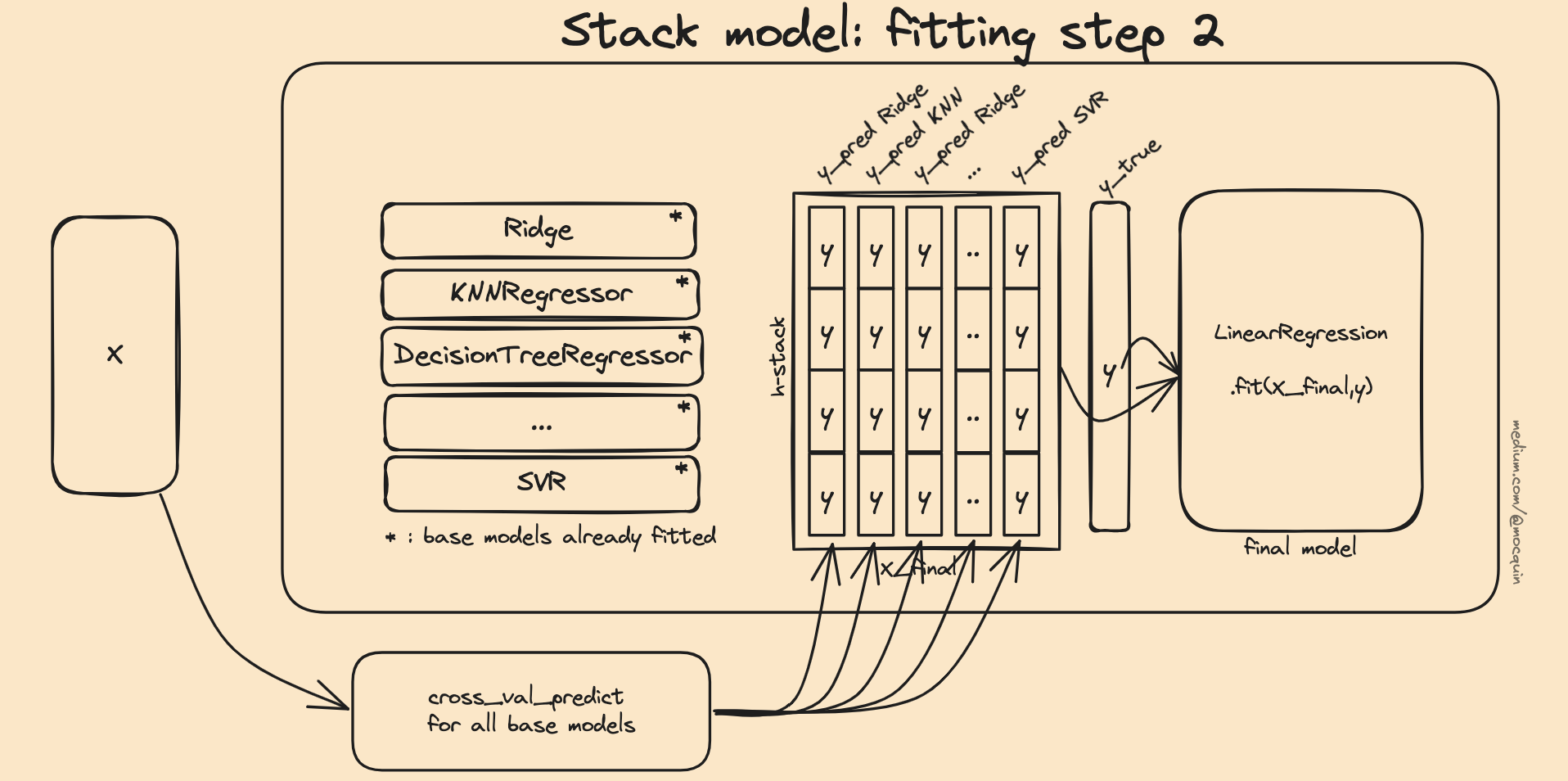
This way, the final estimator is fitted with predictions from the base models on samples that were not already seen by the base models.
Another way to see this fitting procedure is to represent the intermediate 2D dataset X_final from the cross-validation folds decomposition: the X dataset is split into N folds (X_train, X_test, y_train, y_test). The folds must respect the "partition" criteria, such that each individual sample is used only once a test set. For each of those splits, a copy of unfitted-base models is fitted using .fit(X_train, y_train), and the corresponding predictions are computed using .predict(X_test). This way, we get the y_pred for all base models, and for all splits. The final X_train is simply the vertical concatenation of the predictions for all splits.
Restacking
The stacking architecture allows for an additional customization of the model, you can see this as a hyperparameter that allows us to tune how the model works. The idea is really simple: in addition to the horizontally-stacked predictions of the base models, the original input X dataset is also added to the input of the final estimator. This way, the final estimator can find more information in the data, including both the predictions of the base models and the original data. Put another way, the stacking model's complexity is increased, by increasing the number of features of the input of the final model.
In scikit-learn, this is done through the passthrough=True parameter of the stack models.

Obviously, the X matrix is added to X_final both at fit time and predict time.
Multilayer
The way a stacking model is designed allows to simply create additional stacks, creating even more complex models. This can be done by nesting stack models, where any new stack is set as the final estimator of the previous stack. Note that this will increase the complexity of the model, at the cost of increased fit/predict time and potential overfitting.
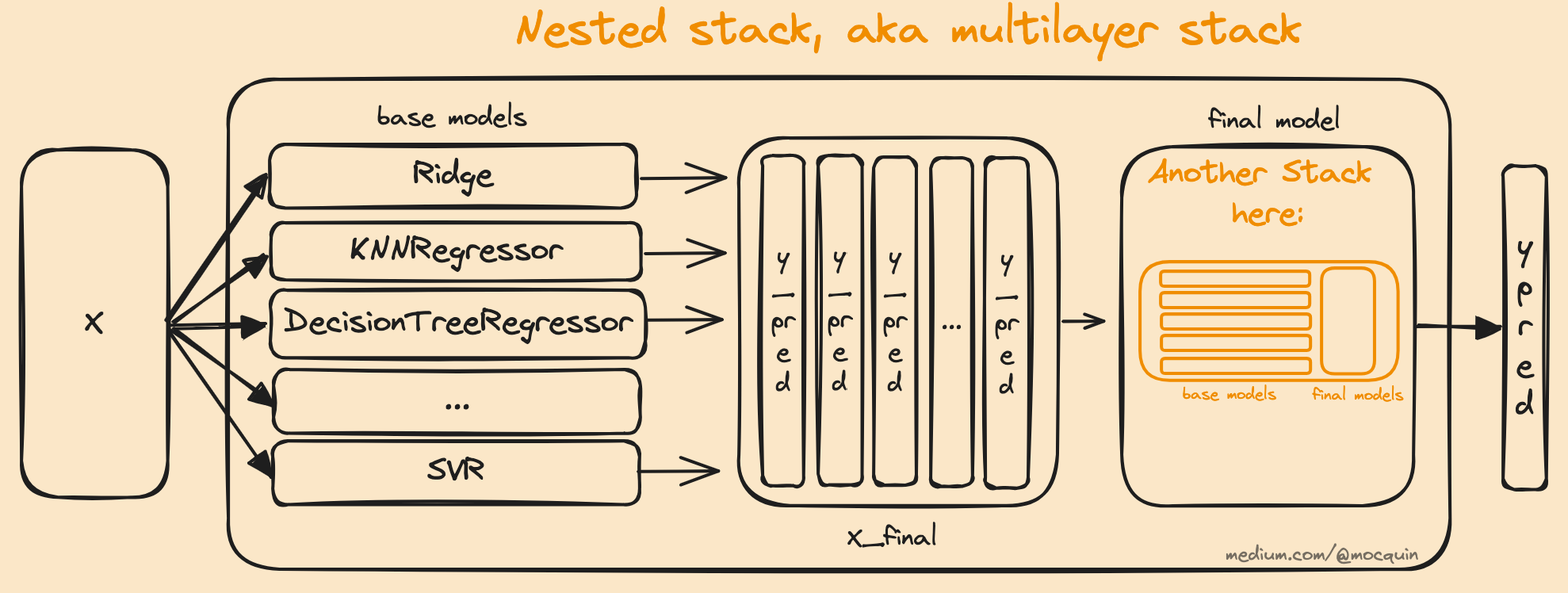
Tuning stack model
As mentioned above, stacking aims at keeping the best out of each base models, so they can compensate each other weaknesses. This means if all models perform equally on the same samples, the stack model won't be any better, so we can optimize the stack model by using base models that perform differently, ideally on various topological areas of the dataset.
Hence it can be a good idea to inspect how the base model performs and if their predictions errors are correlated or not. If 2 models share pretty much the same errors, one can probably be discarded – decreasing the computational complexity while keeping overall performance.
As a stack wraps all the base models and final model, it inherits all their hyperparameters. Since we're interested in the performance of the stack and not rigorously in the base models performances, their hyperparameter must be tuned from the stack context, not before stacking them. In other words, the base models can perform better alone with hyperparameter=A, but the stack performance might be better with hyperparameter=B.
Finally, using passthrough=True or False is another way to tune the stack model.
Overall, you should always check if any base model performs as well as the stack; if so, either discard or tune the stack as its high computational complexity must come with non-insignificant performance increase.
Stacking is a form of ensemble models, hence having imperfect individual model is not always a bad thing, the goal being that models performances complement each other – the same way weak learners are combined to create a bigger better model.
In practice, a stacking predictor predicts as good as the best predictor of the base layer and even sometimes outperforms it by combining the different strengths of the these predictors. However, training/predicting with a stacking predictor is computationally expensive.
Stacking with scikit-learn
Now that we know all about stacking, let's see how to use it with scikit-learn. The only thing you have to remember is that in scikit-learn, stacking is implemented as a model/meta-model:
- it is a model in the sense it has .fit and .predict methods
- it is a meta-model in the sense it takes other models as inputs
Scikit-learn provides a stacking model both for classification and regression, in the ensemble module. Let's see a very simple example for regression:
Python">%matplotlib qt
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
from sklearn.datasets import load_iris, make_moons, make_circles
from sklearn.model_selection import StratifiedKFold, train_test_split, cross_validate
from sklearn.svm import SVC, LinearSVC
from sklearn.naive_bayes import GaussianNB
from sklearn.neighbors import KNeighborsClassifier
from sklearn.linear_model import LogisticRegressionCV, LogisticRegression
from sklearn.ensemble import StackingClassifier
X, y = make_circles(n_samples=500, noise=0.3, factor=0.5, random_state=1, shuffle=True)
# We use 3 base models
base_models = [
('knn', KNeighborsClassifier(n_neighbors=3)),
('logreg', LogisticRegression(max_iter=1000)),
('svc', SVC(C=0.05)),
]
# Create a stack with the base models, and a LogisticRegression as the final estimator
stack = StackingClassifier(
estimators=base_models,
final_estimator=LogisticRegressionCV(max_iter=1000)
)
restack = StackingClassifier(
estimators=base_models,
final_estimator=LogisticRegressionCV(max_iter=1000),
passthrough=True,
)
# Then we have a nice list to compare all models
models = base_models + [('stack', stack), ('restack', restack)]
X_train, X_test, y_train, y_test = train_test_split(X, y, stratify=y)
for name, model in models:
model.fit(X_train, y_train)
# decision boundary for stacking classifier
x_min, x_max = X[:, 0].min() - 1, X[:, 0].max() + 1
y_min, y_max = X[:, 1].min() - 1, X[:, 1].max() + 1
xx, yy = np.meshgrid(np.arange(x_min, x_max, 0.2),
np.arange(y_min, y_max, 0.2))
fig, axes = plt.subplots(1, len(models), sharex=True, sharey=True)
for ax, (name, model) in zip(axes, models):
Z = model.predict(np.c_[xx.ravel(), yy.ravel()])
Z = Z.reshape(xx.shape)
ax.contourf(xx, yy, Z, alpha=0.8)
ax.scatter(X_test[:, 0], X_test[:, 1], c=y_test, edgecolors='k')
ax.set_title(f"{name} score={model.score(X_test, y_test):.2f}")
ax.set_xlabel("Feature 1")
ax.set_ylabel("Feature 2")
fig.tight_layout()For completness, I added a restacked version of the stack. As the plot shows, combining the base models brings the performance of the stack a bit above the best performance among the base models. Using restacking brings another little increase in performance.

Note that the above just demonstrates how to create a stack models- actual performance estimation would necessitate tuning and cross-validation.
Stacking "from scratch"
Now let's see a simple implementation of stacking, using scikit-learn API. This just a toy example to demonstrate how stacking is not that complicated. Except for learning/explaning purposes, you should use scikit-learn's implementation!
import numpy as np
from sklearn.datasets import load_diabetes
from sklearn.ensemble import RandomForestRegressor
from sklearn.linear_model import Ridge
from sklearn.model_selection import cross_validate
from sklearn.base import BaseEstimator, RegressorMixin, TransformerMixin, clone
from sklearn.model_selection import cross_val_predict
class HomeMadeStackingRegressor(BaseEstimator, RegressorMixin, TransformerMixin):
def __init__(self, base_estimators, meta_estimator):
self.base_estimators = base_estimators
self.meta_estimator = meta_estimator
def fit(self, X, y):
self.base_estimators_ = [clone(est) for est in self.base_estimators]
self.meta_estimator_ = clone(self.meta_estimator)
# Fit base estimators independantely
for est in self.base_estimators_:
est.fit(X, y)
# Generate X_final feature dataset for the final estimator
# as the concatenation of the cross_val_predict restults of the base estimators
X_final = np.array([cross_val_predict(est, X, y, cv=5) for est in self.base_estimators_]).T
# Fit final estimator
self.meta_estimator_.fit(X_final, y)
return self
def predict(self, X):
meta_features = np.array([est.predict(X) for est in self.base_estimators_]).T
return self.meta_estimator_.predict(meta_features)
boston = load_diabetes()
X, y = boston.data, boston.target
base_estimators = [RandomForestRegressor(n_estimators=20, max_depth=3, random_state=1), Ridge()]
meta_estimator = Ridge()
stack = HomeMadeStackingRegressor(base_estimators, meta_estimator)
models = list(zip(['rf', 'ridge'], base_estimators)) + [('stack', stack)]
results = []
for name, basemodel in models:
cv_results = cross_validate(basemodel, X, y, return_estimator=True, return_train_score=True)
df = pd.DataFrame.from_dict(cv_results)
df.reset_index(names="run", inplace=True)
df["model"] = name
results.append(df)
cv_results = pd.concat(results).reset_index(drop=True)
cv_results_melt = cv_results.melt(id_vars=["model", "run"], value_vars=["test_score", "train_score", "fit_time", "score_time"], var_name="metric", value_name='value')
sns.catplot(cv_results_melt, y="model", x="value", kind="bar", hue="model", col="metric", sharex=False)
As you can see, the test score of the stack is better than any of its base models. On the other hand it comes at higher fit time.
Wrap-up
Here's what you should remember about stacking:
- it is an ensemble technique that uses a final model to combine the predictions of the base models
- the final model uses the horizontal stack of the predictions of the base model as its input
- it works best when the base models are different and compensate each other weaknesses. It should perform at least better than the best of the base models.
- it can (and should) be tuned, using the base and final models hyperparamters, as well as its passthrough parameter to enable restacking or not
- the fitting process involve using a cross-validation scheme to fit the final estimators (the base estimators are fitted independentely as usual)
Check out my other posts if you liked this one:

