Two Common Pitfalls to Avoid When Doing Cross-Validation

Author:Murphy | View: 29877 | Time: 2025-03-22 21:38:31

Cross-validation is an essential technique for data scientists, but it's easy to misuse.

In this article, I'll highlight two mistakes I regularly see and the concepts you need to combat them:

Nested cross-validation
Time series cross-validation

Learning these techniques helped me get my first job in Data Science, and, if you can master them, you'll safeguard yourself from making silly mistakes when building ML models.

But first, a recap: what's the point of cross-validation?

The basic idea of Machine Learning is: fit a model on a "training" data set and evaluate its performance on a separate held-out "testing" data (which is supposed to simulate how your model will perform in the real world):

from sklearn.model_selection import train_test_split
from sklearn.linear_model import LogisticRegression
from sklearn.metrics import roc_auc_score
from sklearn.datasets import make_classification

# Example dataset
X, y = make_classification(n_samples=1000, n_features=20, random_state=42)

X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2)

clf = LogisticRegression()
clf.fit(X_train, y_train)
y_pred = clf.predict(X_test)

rocauc = roc_auc_score(y_test, y_pred)

But there's a problem with the simple train-test split approach.

When you use a single train-test split (as above), it's possible that your X_test and y_test splits won't be representative of the type of data your model will encounter in production. This is a problem because it means your model's performance on the test split might not be a reliable estimate of performance in production.

Cross-validation is a neat way to train robust models

The solution to this is to use cross-validation, which involves:

Creating multiple train-test splits,
training and evaluating your model on each of these splits separately, and
calculating the average performance across all testing splits.

This will give you a much more reliable estimate of your model's real-world performance. (The fancy way of saying this is that cross-validation helps you "estimate the generalization error of the underlying model".)

Here's a visual comparison of simple evaluation versus k-fold (5-fold) cross-validation:

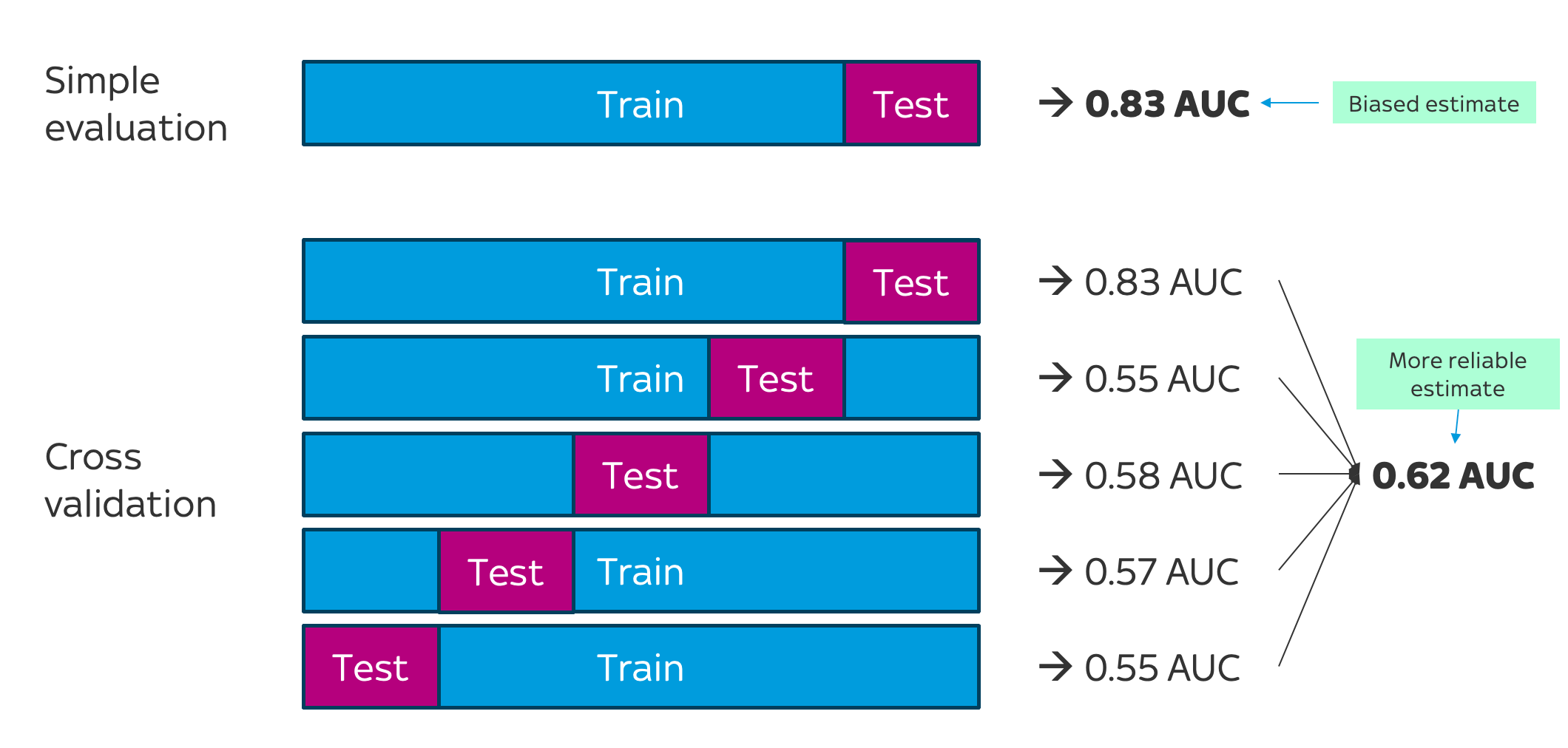
As the image shows, a cross-validation process always starts by creating the different train-test splits. In our case, we're using 5-fold cross-validation, so we'll create 5 versions of the training and testing data.

Next, for each split, we train the model on the Train split and calculate its performance on the Test split. Finally, we compute the average score across all Test splits. This gives us a much more reliable/realistic picture of our model's ability, which is less likely to be biased by the particular splitting strategy we used.

Scikit-learn's cross_val_score function is a nifty way to achieve this in a single line of code:

from sklearn.model_selection import train_test_split, cross_val_score
from sklearn.linear_model import LogisticRegression

clf = LogisticRegression()
scores = cross_val_score(clf, X, y, cv=5, metric='roc_auc')

So… what's the problem?

Cross-validation seems great, doesn't it?

Unfortunately, in my experience as a data scientist, I've found that using a simple cross-validation strategy like k-fold (as shown above) or leave-p-out is rarely enough to ensure that my models are reliable.

In the next part of this article, I'll walk through three common mistakes I've seen and the advanced techniques you need to combat them.

Mistake #1: Not using nested cross-validation when tuning hyperparameters

When tuning the hyperparameters of your model, it's important that you don't use the final test set to repeatedly evaluate different model configurations (because this would incur a subtle form of leakage).

What do I mean by this? Let's say you split your data into a single Train set and a single Test set:

from sklearn.model_selection import train_test_split

X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2)

You start by initialising a model with the default hyperparameters, train it on your Train set, and evaluate it on your Test set:

from sklearn.ensemble import RandomForestClassifier
from sklearn.metrics import roc_auc_score

# Initialise model with default hyperparameters
clf = RandomForestClassifier()

# Fit the model to your `Train` set
clf.fit(X_train, y_train)

# Generate predictions on `Test` and evaluate
y_pred = clf.predict(X_test)
print(roc_auc_score(y_test, y_pred))

# 0.73

0.73 AUC – not too shabby.

However let's say that, after reviewing those results, you decide to try a slightly different hyperparameter configuration by setting n_estimators to 500. You retrain the (new) model on Train, and again evaluate it on Test:

# Initialise the model with a new `n_estimators` hyperparameter value
clf = RandomForestClassifier(n_estimators=500)

# Fit the model to your `Train` set
clf.fit(X_train, y_train)

# Generate predictions on `Test` and evaluate
y_pred = clf.predict(X_test)
print(roc_auc_score(y_test, y_pred))

# 0.74

Then, after seeing those results, you pick a third hyperparameter configuration, retrain on Train, and evaluate on Test:

# Initialise the model with a new `n_estimators` hyperparameter value
clf = RandomForestClassifier(n_estimators=1000)

# Fit the model to your `Train` set
clf.fit(X_train, y_train)

# Generate predictions on `Test` and evaluate
y_pred = clf.predict(X_test)
print(roc_auc_score(y_test, y_pred))

# 0.75

We've reached 0.75 AUC – that's great news!

Or is it?

On the surface, it looks like we've improved our model.

But do you see the problem?

We used scores from the Test set to inform our choice of hyperparameters. This is a subtle form of leakage, and it's a problem because we've picked hyperparameters tailored to our particular Test set, without knowing whether those are the best hyperparameters for generalised real-world performance. We have indirectly "leaked" some information about the Test set to our model; information which wouldn't be available in production, and therefore shouldn't have been used.

Having a validation AND held-out test set help safeguard against this:

For each hyperparameter configuration, you train the model on the Train set, evaluate it on the Val set, and then, once you've found the optimal hyperparameters, you train a model using those hyperparameters and evaluate it on your final "held-out" Test split (which the model hasn't yet seen). This helps ensure the integrity of your training process and prevents any pesky leakage.

The importance of nested cross-validation

So far, this has been pretty straightforward – Machine Learning 101!

But this is where things get interesting.

Again, we have the problem that the particular train-validation split we choose might affect the hyperparameters we select.

To safeguard against this, we can use cross-validation to find the optimal hyperparameters:

*This is just one way to get from cross-validation to a final model. Other strategies are possible – take a look at this excellent post by Christoph Molnar if you fancy learning more. Image by author

But, while this is better than a simple Train–Val–Test splitting strategy, it's still not ideal, because the purple Test split might not be representative of the data we'll encounter in the real world.

We're back to the same problem we had in the simple (non-cross-validation) evaluation approach.

For this reason, we might want to use nested cross-validation, where we have one cross-validation loop for selecting the hyperparameters, and one for evaluating the model:

Nested cross-validation. Image by author

Here's scikit-learn code which demonstrates this:

# Hyperparameters to tune
param_grid = {
    'pca__n_components': [2, 5, 10],
    'classifier__n_estimators': [50, 100],
    'classifier__max_depth': [None, 10, 20],
}

# Inner CV for hyperparameter tuning
grid_search = GridSearchCV(RandomForestClassifier(), param_grid, cv=5)

# Outer CV for model evaluation
outer_cv = KFold(n_splits=5)

# Nested CV
nested_score = cross_val_score(grid_search, X, y, cv=outer_cv)

print("Nested CV Score: ", nested_score.mean())

Nested cross-validation is a fiddly topic, but it's a fantastic skill for a data scientist to have. If you'd like to learn more, I'd recommend this article, which has a nice implementation of nested cross-validation incorporating a Pipeline (my favourite scikit-learn hack):

A Guide to Nested Cross-Validation with Code Step by Step

Mistake #2: Incorrect splitting of time series data

Time series data require special treatment.

A defining feature of time series data is that they're autocorrelated – i.e., the time series is linearly related to a lagged version of itself. (This is a fancy way of saying that observations made close together tend to be similar.)

This is a problem because, if your training data set contains records which occur later than your testing data set, you're allowing your model to "peak" at useful information which wouldn't be available in production. We don't want our model to learn using information from the future; we want it to learn the trend using information from the past.

For this reason, we have to use a special splitting strategy when performing cross-validation. Here's a quick visualisation of what we're aiming for:

First, we define our held-out Test set (in the diagram above, the Test set spans four weeks from week 9 20224 to week 13 2024). This is the final "out-of-time" split which we will use to estimate our model's real-world performance.

Next, we create our k cross-validation splits (i.e., we create k versions of the Train and Validation sets). Each Train split begins at week 1 2023, and goes up to the week before the Val split.

Scikit-learn provides a handy TimeSeriesSplit class which helps you do this:

from sklearn.model_selection import TimeSeriesSplit

tscv = TimeSeriesSplit(n_splits=5)

scores = []

for i, (train_index, val_index) in enumerate(tscv.split(X)):
    # If you want to visualise the folds
    # print(f"Fold {i}:")
    # print(f"  Train: index={train_index}")
    # print(f"  Val:  index={val_index}")

    train_X = X_train.loc[train_index]
    train_y = y_train.loc[train_index]
    val_X = X_train.loc[val_index]
    val_y = y_train.loc[val_index]

    clf = RandomForestClassifier()

    # Fit the model to your `Train` set
    clf.fit(train_X, train_y)

    # Generate predictions on `Test` and evaluate
    y_pred = clf.predict(val_X)
    scores.append(roc_auc_score(val_y, y_pred))

print(np.mean(scores))

(Note that I've not included nested cross-validation here – there's only a single held-out Test split, which contains 4 weeks of data. This is partly for brevity and partly to illustrate that you don't always need to use every tool in your toolbox. The appropriate cross-validation strategy will always depend on the situation.)