What Makes A Strong AI?
What Makes A Strong AI?
We are at the last article reading Judea Pearl's inspiring "The Book of Why," and it will mostly focus on mediators and how to combine causality with big data to derive trustworthy conclusions. I will also summarize what makes a strong AI in the end based on the whole book.
Mediators
We have briefly talked about mediation in the previous articles. We mentioned it is important to identify mediators not only because we shouldn't treat them as confounders, since conditioning on them will block the causal effect completely or partially, but also in proper cases, we can use mediators for front-door criterion when unobserved confounders exist.

In this section, we will dive deeper into different examples of mediators and understand how to properly define direct causal effect, indirect causal effect, and total causal effect when mediators exist.
In history, scurvy had always been the most terrifying disease for sailors. Before vitamins were discovered and properly named, scientists struggled to figure out how to prevent sailors from getting scurvy. They first asked what is the cause – why did some sailors get scurvy and some don't? Having observed that citrus fruits helped reduce scurvy, they needed to explain why citrus fruits help prevent scurvy, which led to the discovery of Vitamin C.

Mediators provide answers to the second "why" question. In this example, Vitamin C is the mediator for the citrus fruits to take into effect, and citrus fruits have no direct effect on scurvy. If we dry or boil these fruits, it won't help prevent scurvy anymore.
Unlike the previous example, in many cases, there are two paths for a cause to effect. The route that connects cause to effect directly represents the direct causal effect. There may exist another route that connects the cause and effect through a mediator, which produces the indirect causal effect.

Thus, a one-unit change in the cause will impact the outcome variable in two paths, and only the total effect is what we observe. In this section, we will explore some examples to see why it is important to isolate the direct and indirect effects from the total effects. To estimate the direct and indirect effects, we need to borrow the concept of counterfactuals from the last article, and we will discuss more details in the next section.
Algebra for All
Chicago Public School system once introduced an "Algebra for All" program that required all ninth graders to take college-prep math courses. To understand whether taking these courses improved students' test grades causally, we first need to remove confounders, like other curriculum changes that would also impact students' test grades. After careful consideration, researchers found no significant improvement in test scores. However, before jumping into claiming the program is not effective, the researcher examined more on how can introducing new courses impact students' grades. It turned out that "Algebra for All" not only changed the curriculum but also changed the teaching environment where lower-achieving students are mixed with higher-achieving students during class. Larger class size not only reduces teaching efficiency but also discourage lower-achieving students from catching up. Thus, we have the following causal graph when adding "Environment" as a mediator:

Here, the direct effect of "Algebra for All" on learning is positive, but the indirect effect through the mediator "Environment" is negative. Thus, the total effect without distinguishing the direct and indirect effects will more than likely be minimal.
In this case, the researcher estimated the direct effect and indirect effect individually. Since the results did show a positive direct effect and a negative indirect effect, the researcher concluded that "Allegra for All" should increase students' test scores if maintaining the pre policy classroom environment.
Revisit The Smoking Gene
From previous articles, we might be very familiar with the debate happening when analyzing the causal effect of smoking on lung cancer. One confounder that was brought into the front stage was the smoking gene:

With progress in medical research, genomics experts did locate the smoking gene, what they called "Mr. Big," because of its strong association with lung cancer. The finding of the smoking gene shouldn't overshadow smoking as a causal factor in lung cancer. Nevertheless, even a double dose of the smoking gene doesn't double the risk of getting lung cancer.
How can the discovery of the smoking gene help us other than serving as a confounder? If we make a small shift on the same causal graph and treat smoking gene as the treatment and smoking as a mediator to lung cancer:

With this change, as Pearl mentioned, we can estimate the smoking gene's direct effect: Does the smoking gene make lung cells more vulnerable to cancer? We can also estimate the smoking gene's indirect effect: Does the smoking gene make people smoke more and inhale harder?
Comparing whether direct or indirect is higher will give different action guidance. If the direct effect is higher, then people with the smoking gene should receive extra screening for lung cancer throughout their lives. On the contrary, if the indirect effect is higher, health professionals should pay more attention to intervening in the smoking behaviors of individuals carrying the smoking gene.
Estimate Direct and Indirect Effects
After demonstrating the importance of isolating direct effect and indirect effect, let's move to how to estimate the causal effect, a Rung 2&3 question, from Rung 1 data.
For a long period of time, the standard way of estimating direct and direct effects follows simple rules. Supposed we have the following causal diagram with the coefficients representing the causal effects:
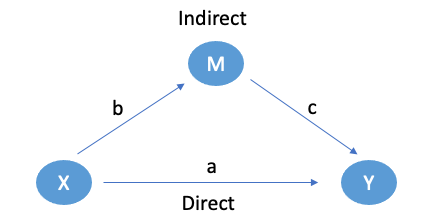
The direct effect would be a, and the indirect effect would be bc. Thus, ** the total effect with one unit increase in the cause is **a+bc. However, there are some assumptions needed to arrive at this conclusion.
The first assumption is that all variables follow linear relationships. There is a simple example in Pearl's book that shows that if we change the linear relationship simply to binary conditions, this would not work. Moreover, in essence, a linear relationship would not be able to capture the case when there are interactions between the cause and the mediator.

No interaction is a strong assumption. Take "Algebra for All" as an example. It is very likely that a more challenging curriculum, combined with a less supportive classroom environment, will be more discouraging for low-achieving students to get better grades. The linear system would not be able to reflect this interaction.
Another assumption made here is this equation:
Total Effect = Direct Effect + Indirect Effect
This sounds very logical. What's the problem with this? In the book, Pearl gives an example. Suppose we are estimating the efficiency of a drug that doesn't have a direct effect but has an indirect effect through stimulating enzymes.

We know the total effect is positive because the drug is effective. The direct effect is zero because if we disable the enzyme, the drug will not work.
When estimating the indirect effect, and we block the drug and artificially get the enzyme, the disease would not be cured because it would only work if we combine the drug and the enzyme.
This is another example of interaction between cause and mediator. In this case, the total effect is positive, but both direct and indirect effects are zeros.
The essence of the challenges, in my opinion, is how to define the quantity of mediator M when calculating indirect effect, especially when there are interactions between X and M.
We know the value of M when there is treatment, what would have been the value of M without the treatment? And how does this value differ across individuals?
These questions all point to the concept we have discussed in the previous chapter – – counterfactuals. If the direct effect is
The effect remaining after holding the mediator fixed
The definition Pearl gives for indirect effect is more complicated:
The indirect effect of X on Y is the increase we would see in Y while holding X constant and increasing M to whatever value M would attain under a unit increase in X.
The key here is we first need to know what M would have been when X changes before we know it's indirect impact on Y. With counterfactuals embedded, Pearl presents the two equations to estimate direct and indirect effects. The natural direct effect (NDE) is:

Here we make the mediator fixed at M0, a value that M would have been given that X takes the value 0. In the "Algebra for All" example, M would be the teaching environment, or specifically, the classroom size when there is no curriculum change. We are comparing the direct impact of do(X=0) and do(X=1) on outcome Y=1.
The natural indirect effect (NIE) is:

Here we ensure do(X=0) on both terms to ensure no direct effects. Note we make the mediator take the value of M1 in the first term, which is what M would be given that X=1. For example, what the classroom size would have been given that the "Algebra for All" program had launched. In the second term, however, the mediator takes the value of M0. The natural indirect effect basically calculates a difference that is only deduced by the change in the value of the mediator, and how much the mediator will change from M0 to M1 depends largely on the causal relationship between X and M.

Arriving at these equations was not an easy task. There are so many more details to this journey, with generations of researchers' efforts. You can refer to Pearl's book for more.
Causality and Big Data
All throughout the book, Pearl tries to prove that only relying on data without understanding causality is not enough to derive trustworthy results. However, data and models are never enemies. In fact, having data is the first step to arrive at any conclusion. For the last chapter of the book, Pearl explores the opportunities we have combining causality and big data:
Causal inference permits us to screen off the irrelevant characteristics and to recruit these individuals from diverse studies, while Big Data allows us to gather enough information about them.
To illustrate how we can combine causal models and data from different studies to get new insights, Pearl shows an example to analyze an online advertisement(X) on the likelihood that a consumer will purchase the product(Y). If the company already has data from different cities' previous campaigns, like in Los Angeles, Boston, Toronto, etc, and is looking for ways to generalize the results to the population in Arkansas, with the help of causal diagrams, there might be ways we can measure the effect in new population without all the new data, or any new data.
Specifically, let's look at the causal diagram showing how the online campaign causes sales to increase:

There is Z representing confounders. In this case, Z could be age, showing that some products are only preferred by certain age groups, like young people, and they also happen to be more exposed to online promotions. W represents the mediator for X to affect Y. For example, it could be the click rate on a link that converts customers from seeing an advertisement to purchasing the product.
In the easiest case, suppose we already have survey data from Boston from their past campaigns and the only difference between Boston and Arkansas population is the rate of car ownership. Let S represent the difference between these two populations, and we can revise the causal diagram:

If the causal diagram holds, it means the effect of the Arkansas online advertisement should be the same as in Boston since S and V will not affect the causal path X->W->Y because it's blocked by the collider Z.
In a more complicated case, suppose we have survey data from Los Angeles, and the difference is that the LA population might be younger. The revised causal diagram would be:

In this case, S is impacting the X->Y causal effects through the confounder Z. Thus, we need to reweigh the data in LA to account for the different age structures.
If we cannot measure Z in Arkansas, we can instead look for randomized trials that might have been done in other cities and see whether we can adjust for Arkansas. For example, if we have randomized trials from Toronto, and the only difference is that Toronto has a higher click-through rate:

Since this is a randomized experiment, we could remove the path between X and Z. By just collecting data on X, W, and Y in Arkansas, we can estimate the causal impact with the results from Toronto.
Even in the case where S impacts Y directly, i.e., the product is more desirable in this city:

Again, this is from experiment data so we can remove the link between X and Z. Even if the difference S directly impacts Y, we can still use this city's estimation on P(W|X) to contribute partially to the overall causal impact.
All these examples show that Big Data is our friend. Combining with reasonable causal structure, we know which sets of data are desired to derive trustworthy causal effects, which saves us trouble from always running randomized trials or collecting as much data as possible.
What Makes A Strong AI
In the last two months of 2023, we have been indulging in the world of causality through reading "The Book of Why" by Judea Pearl. Time flies. We said goodbye to 2023 and to "The Book of Why." However, this won't be the end of exploring the fascinating world of causality and pushing the boundaries of Artificial Intelligence. Pearl illustrates what makes a strong AI in every chapter, and I briefly talked about in my previous articles:
A strong AI never makes decisions only based on correlations. It needs to step up from Rung 1, "seeing," to Rung 2, "intervening," and Rung 3, "imagining." Not only do they need to know what the patterns were from the past, but they also need to understand why these patterns came up to make intelligent predictions.
A strong AI never makes decisions based on rules. Instead, it draws conclusions following causal structures. In addition to having the ability to derive the probability of an outcome based on the probability of cause, it also knows to update its belief that given the outcome, what's the probability of cause. With the help of causal diagrams, a strong AI goes beyond the Bayesian network and is capable of finding Causality in observational studies.
A strong AI knows how to distinguish spurious correlations and true causalities. It will not mistake collider bias as causation, and will not eliminate causal impacts by conditioning on mediators.
A strong AI resembles human brains when categorizing causes into necessary causes and sufficient causes. Although multiple variables can be the causal factors for an outcome, human brains automatically "rank" these factors based on how rare events happen and what are the action points. A strong AI not only looks for why but also ranks the why.

In the last two chapters, Pearl also mentioned the importance of transparency in the AI decision making process. Just like we want to know the why about everything, we want to know why the AI makes this decision.
Not all AI researchers are fans of transparency. In Pearl's book, he mentions:
The field at that time was divided into "neats" (who wanted transparent systems with guarantees of behavior) and "scruffies" (who just wanted something that worked)
Although scruffies could get temporary solutions, a strong AI is a transparent AI so that humans can better coach it, tailor it the way we like, and even learn from it. Ultimately, humans always long for effective communication. As Pearl said, it would be "quite unfortunate" if we cannot hold meaningful conversations with AI.
2023 was a revolutionary year. With the widespread use of Generative AI, we are hopeful and simultaneously intimidated by what AI can do, just like when we were facing any new technology in history. Pearl is optimistic, he said at the end of the book:
Once we have built a moral robot…… we will be able to depend on our machines for a clear-eyed and causally sound sense of justice…… Such a thinking machine would be a wonderful companion for our species and would truly qualify as AI's first and best gift to humanity.
However, having data, no matter how much more, will not enable machines to resemble human-level intelligence without embedding causal models, with which, AI can "think about own intentions and reflect on its own mistakes." The AI that climbs above Rung 1 to make Rung 2 interventions and Rung 3 counterfactuals. And this is how we make a strong AI.
Thanks for reading. This concludes the Read with Me series. What an amazing collective learning experience! The good news is that I plan to publish a bonus article in two weeks to officially close this series.
If interested, subscribe to my email list to get notified of my future articles. If you like this article, don't forget to:
- Check my recent articles about the 4Ds in data storytelling: making art out of science; continuous learning in data science; how I become a data scientist;
- Check my other articles on different topics like data science interview preparation; causal inference;
- Subscribe to my email list;
- Sign up for medium membership;
- Or follow me on YouTube and watch my most recent YouTube videos:

